


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源:不详 题型:填空题
 ”类比“若
”类比“若 为三个向量,则
为三个向量,则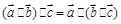 ”;②设圆
”;②设圆 与坐标轴的4个交点分别为A (x1,0)、B (x2,0)、C (0,y1)、D (0,y2),则
与坐标轴的4个交点分别为A (x1,0)、B (x2,0)、C (0,y1)、D (0,y2),则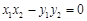 ;③在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”;④在实数列
;③在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”;④在实数列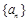 中,已知a1 = 0,
中,已知a1 = 0,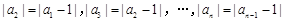 ,则
,则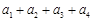 的最大值为2.上述四个推理中,得出的结论正确的是_____________(写出所有正确结论的序号).
的最大值为2.上述四个推理中,得出的结论正确的是_____________(写出所有正确结论的序号).查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
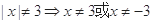 ;
;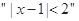 是
是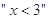 的充分不必要条件
的充分不必要条件| A.①④ | B.②③ | C.②④ | D.③④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
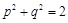 ,则
,则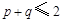 ”的逆否命题是“如果
”的逆否命题是“如果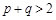 ,则
,则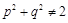 ”;
”;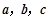 为非零的平面向量.甲:
为非零的平面向量.甲: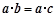 ,乙:
,乙: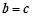 ,则甲是乙的必要条件,但不是充分条件;
,则甲是乙的必要条件,但不是充分条件;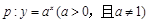 是周期函数,
是周期函数,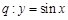 是周期函数,则
是周期函数,则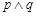 是真命题;
是真命题;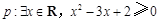 的否定是:
的否定是: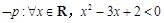 .
.| A.①② | B.①④ | C.①②④ | D.①③④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
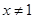 ,则
,则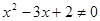 ”的逆否命题: “若
”的逆否命题: “若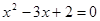 ,则
,则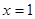 ”.
”.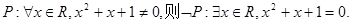
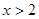 ”是“
”是“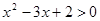 ”的充分不必要条件.
”的充分不必要条件.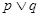 为真命题,则
为真命题,则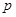 ,
,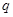 均为真命题.
均为真命题.| A.4个 | B.3个 |
| C.2个 | D.1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com