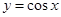Question

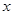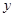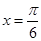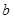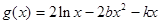设曲线与轴、轴、直线围成的封闭图形的面积为，若在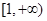上单调递减，则实数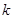的取值范围是     。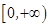

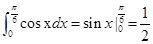Answer 1

试题分析：由题意，先用定积分求出b，再由g（x）=2lnx-2bx²-kx在[1，+∞）上单调递减，利用其导数在[1，+∞）上恒小于0建立不等式求出实数k的取值范围．根据题意可知，函数在给定区间上的定积分,∴g（x）=2lnx-x²-kx∴g′（x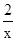）=-2x-k,∵g（x）=2lnx-2bx²-kx在[1，+∞）上单调递减，∴g′（x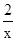）=-2x-k＜0在[1，+∞）上恒成立,即k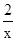＞-2x在[1，+∞）上恒成立,∵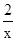-2x在[1，+∞）上递减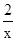，∴-2x≤0,∴k≥0,由此知实数k的取值范围是[0，+∞）,故答案为：[0，+∞）．
点评：本题考查定积分在求面积中的应用，解题的关键是利用定积分求出b，再利用导数与单调性的关系将函数递减转化为导数值恒负，由此不等式恒成立求出参数的范围，本题综合性很强，需要多次转化变形，运算量较大，解题时一定要注意变形正确，运算严谨，避免因变形，运算出错．