
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知如图所示的程序框图(未完成),设当箭头a指向①时,输出的结果为S=m,当箭头a指向②时,输出的结果为S=n,则m+n的值为________.
已知如图所示的程序框图(未完成),设当箭头a指向①时,输出的结果为S=m,当箭头a指向②时,输出的结果为S=n,则m+n的值为________.查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
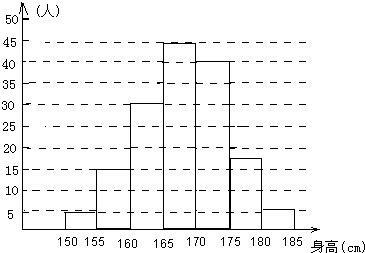 抽取某校学生的一个容量为150的样本,测得学生身高后,得到身高频数分布直方图如图所示,已知该校有学生1500名,则可以估计出该校身高位于160cm至165cm之间大约有______人.
抽取某校学生的一个容量为150的样本,测得学生身高后,得到身高频数分布直方图如图所示,已知该校有学生1500名,则可以估计出该校身高位于160cm至165cm之间大约有______人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com