
看下面的问题:
1+2+3+…+( )>10000,这个问题的答案不唯一,我们只要确定出满足条件的最小正整数, (括号内填写的数字只要大于或等于
(括号内填写的数字只要大于或等于 即可)即可.试写出寻找满足条件的最小正整数
即可)即可.试写出寻找满足条件的最小正整数 的算法,并画出相应的算法流程图.
的算法,并画出相应的算法流程图.
|
解:算法 1:第一步: p=0;第二步: i=0;第三步: i=i+1;第四步: p=p+i;第五步:若 p>10000,则执行第七步;否则,执行第六步;第六步:回到第三步,重新执行第三步,第四步,第五步. 第七步:输出 i的值.该算法的程序框图如图所示:
算法 2:第一步:取 n的值等于1;第二步:计算 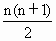
第三步:如果  值大于10000,那么n即为所求,即执行第四步;否则,让n的值增加1,后转到第二步重复操作. 值大于10000,那么n即为所求,即执行第四步;否则,让n的值增加1,后转到第二步重复操作.
第四步:输出 n的值.根据以上的操作步骤,可以画出如图所示的算法流程图.
|
|
由于10000是一个较大的数,用试或猜的办法是行不通的.下面采用累加并应用循环和应用公式并采用循环两种思路解答本题. 算法2的初始值n从1开始,若从一个较大的n的初始值开始,可以减少计算机执行的时间,在算法2中如果n的初始值是一个较大的数,如n=9990,显然1+2+…+9990>10000,算法又应如何设计?请读者自行解决. |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:全优设计选修数学-1-2苏教版 苏教版 题型:044
看下面的问题:
1+2+3+4+…+( )>10 000
这个问题的答案虽然不唯一,我们只要定出满足条件的最小正整数n0,括号内填写的数字只要大于或等于n0即可,试写出寻找满足条件的最小正整数n0的算法并画出相应的算法流程图.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
看下面的问题:1+2+3+…+( )>10000,这个问题的答案不唯一,我们只要确定出满足条件的最小正整数,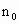 (括号内填写的数字只要大于或等于
(括号内填写的数字只要大于或等于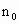 即可)即可.试写出寻找满足条件的最小正整数
即可)即可.试写出寻找满足条件的最小正整数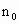 的算法,并画出相应的算法流程图.
的算法,并画出相应的算法流程图.
查看答案和解析>>
科目:高中数学 来源: 题型:
1+2+3+4+…+( )>10 000
这个问题的答案虽然不唯一,我们只要定出满足条件的最小正整数n0,括号内填写的数字只要大于或等于n0即可,试写出寻找满足条件的最小正整数n0的算法并画出相应的算法流程图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com