
在 中,
中, 分别是内角
分别是内角 的对边,且
的对边,且
 ,若
,若
(1)求 的大小;
的大小;
(2)设 为
为 的面积, 求
的面积, 求 的最大值及此时
的最大值及此时 的值.
的值.
(1)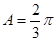 ;(2)当
;(2)当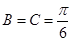 时,
时,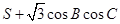 取最大值
取最大值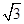 .
.
【解析】
试题分析:本题主要考查解三角形中正弦定理和余弦定理的运用、向量平行的充要条件以及三角形面积公式等数学知识,考查基本运算能力.第一问,先利用向量平行的充要条件列出表达式,然后用正弦定理将角转化为边,再利用余弦定理求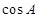 ,注意三角形中角的范围,确定角
,注意三角形中角的范围,确定角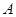 的大小;第二问,用正弦定理表示
的大小;第二问,用正弦定理表示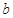 和
和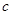 边,然后代入到三角形面积公式中,得到所求的表达式,再利用两角和与差的余弦公式化简表达式,求最值.
边,然后代入到三角形面积公式中,得到所求的表达式,再利用两角和与差的余弦公式化简表达式,求最值.
试题解析:(1)因为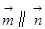 ,所以
,所以
根据正弦定理得 ,即
,即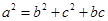
由余弦定理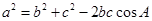 得
得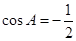 又
又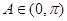 ,
,
所以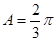 6分
6分
(2)由正弦定理及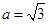 得,
得,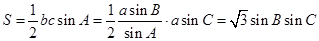
所以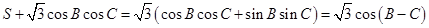
所以当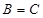 时,即
时,即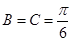 时,
时,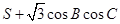 取最大值
取最大值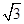 . 12分
. 12分
考点:1.两向量平行的充要条件;2.正弦定理;3.余弦定理;4.三角形面积公式;5.三角函数最值;6.两角和与差的余弦公式.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com