
分析 由题意画出图形,求出$\overrightarrow{AB}、\overrightarrow{OP}$的坐标,代入$\overrightarrow{AB}=λ\overrightarrow{OP}$,结合隐含条件求得实数λ的值.
解答 解:如图,
A(-a,0),B(0,b),F(c,0),
则P(c,$\frac{{b}^{2}}{a}$),
∴$\overrightarrow{AB}=(a,b)$,$\overrightarrow{OP}=(c,\frac{{b}^{2}}{a})$,
由$\overrightarrow{AB}=λ\overrightarrow{OP}$,得$\left\{\begin{array}{l}{a=λc}\\{b=λ\frac{{b}^{2}}{a}}\end{array}\right.$,即b=c,
∴a2=b2+c2=2b2,$\frac{a}{b}=\sqrt{2}$.
则$λ=\frac{a}{b}=\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,训练了平面向量在求解圆锥曲线问题中的应用,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 若p∨q为真命题,则p∧q为真命题 | |
| B. | 若直线ax+y-1=0与直线x+ay+2=0平行,则a=1 | |
| C. | 若命题“?x∈R,x2+(a-1)x+1<0”是真命题,则实数a的取值范围是a<-1或a>3 | |
| D. | 命题“若x2-3x+2=0,则x=1或x=2”的逆否命题为“若x≠1或x≠2,则x2-3x+2≠0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
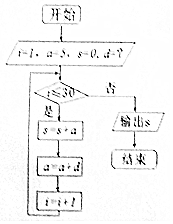 《九章算术》之后,人们学会了用数列的知识来解决问题.公元5世纪中国古代内容丰富的数学著作《张丘建算经》卷上有题为:“今有女善织,日益功疾,初日织五尺,今一月织九匹三丈.问日益几何?”.利用这种思想设计的一个程序框图如图,若输出的S值为九匹三丈(一匹=4丈,一丈=10尺),则框图中d为( )
《九章算术》之后,人们学会了用数列的知识来解决问题.公元5世纪中国古代内容丰富的数学著作《张丘建算经》卷上有题为:“今有女善织,日益功疾,初日织五尺,今一月织九匹三丈.问日益几何?”.利用这种思想设计的一个程序框图如图,若输出的S值为九匹三丈(一匹=4丈,一丈=10尺),则框图中d为( )| A. | $\frac{1}{2}$尺 | B. | $\frac{8}{15}$尺 | C. | $\frac{16}{31}$尺 | D. | $\frac{16}{29}$尺 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向左平移$\frac{π}{3}$个单位 | ||
| C. | 向右平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com