
已知函数 .
.
(Ⅰ)求f(x)的单调递增区间;
(Ⅱ)在△ABC中,三内角A,B,C的对边分别为a,b,c,已知 成等差数列,且
成等差数列,且 =9,求a的值.
=9,求a的值.
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
某同学用“五点法”画函数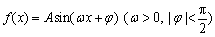 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
|
| 0 |
|
|
|
|
|
|
|
| |||
|
| 0 | 5 |
| 0 |
(Ⅰ)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数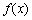 的解析式;
的解析式;
(Ⅱ)令g(x)=f (x+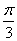 )—1,当x∈[—
)—1,当x∈[— ,
,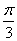 ] 时,若存在g(x)<a—2成立,求实数a的取值范围.
] 时,若存在g(x)<a—2成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙两人同时报考某一所大学,甲被录取的概率为0.6,乙被录取的概率为0.7, 两人是否被录取互不影响, 则其中至少有一人被录取的概率为 ( )
A.0.12 B.0.42 C.0.46 D.0.88
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com