
椭圆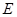 :
: 的右焦点
的右焦点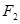 与抛物线
与抛物线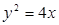 的焦点重合,过
的焦点重合,过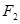 作与
作与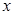 轴垂直的直线
轴垂直的直线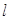 与椭圆交于
与椭圆交于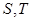 两点,与抛物线交于
两点,与抛物线交于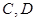 两点,且
两点,且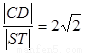 。
。
(1)求椭圆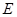 的方程;
的方程;
(2)若过点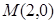 的直线与椭圆
的直线与椭圆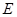 相交于两点
相交于两点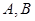 ,设
,设 为椭圆
为椭圆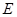 上一点,且满足
上一点,且满足
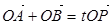
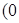 为坐标原点),当
为坐标原点),当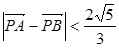 时,求实数
时,求实数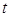 的取值范围。
的取值范围。
(1) 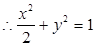 (2)
(2) 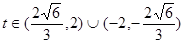
【解析】
试题分析:(1)设椭圆的半长轴、半短轴、半焦距为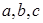 ,则
,则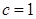 ,且
,且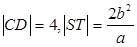 ,
,
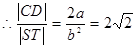 ,又
,又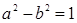 ,
,
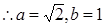 ,
,
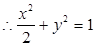 ——————————————————————————————6分
——————————————————————————————6分
(2)由题,直线 斜率存在,设直线
斜率存在,设直线 :
: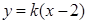 ,联立
,联立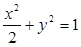 ,消
,消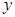 得:
得:
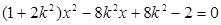 ,由
,由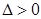 ,得
,得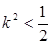 ①————————8分
①————————8分
设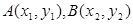 ,由韦达定理得
,由韦达定理得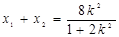 ,
,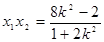
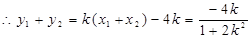 ,
,
则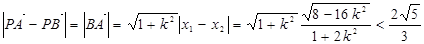
 或
或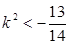 (舍)②
(舍)②
由 ①②得:
①②得: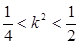 ——————————————————————————11分
——————————————————————————11分
则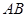 的中点
的中点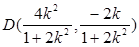
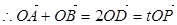 ,得
,得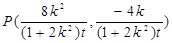 代入椭圆方程得:
代入椭圆方程得:
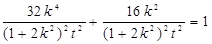 ,即
,即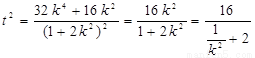
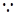
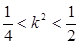 ,
,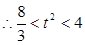 ,即
,即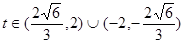 ————————15分
————————15分
考点:椭圆方程,直线与椭圆位置关系
点评:根据圆锥曲线的性质求解椭圆的方程,同时能联立方程组来得到交点坐标的关系,结合韦达定理来分析求解,属于中档题。


科目:高中数学 来源:2012-2013学年福建省三明市毕业班5月质量检查理科数学试卷(解析版) 题型:解答题
已知椭圆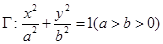 的离心率为
的离心率为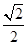 ,且椭圆
,且椭圆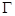 的右焦点
的右焦点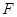 与抛物线
与抛物线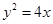 的焦点重合.
的焦点重合.
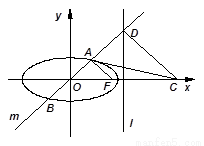
(Ⅰ)求椭圆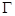 的标准方程;
的标准方程;
(Ⅱ)如图,设直线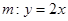 与椭圆
与椭圆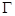 交于
交于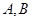 两点(其中点
两点(其中点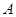 在第一象限),且直线
在第一象限),且直线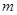 与定直线
与定直线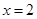 交于点
交于点 ,过
,过 作直线
作直线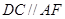 交
交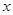 轴于点
轴于点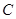 ,试判断直线
,试判断直线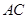 与椭圆
与椭圆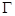 的公共点个数.
的公共点个数.
查看答案和解析>>
科目:高中数学 来源:2014届广东省东莞市高二3月月考文科数学试卷(解析版) 题型:解答题
已知椭圆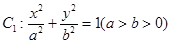 的右焦点
的右焦点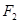 与抛物线
与抛物线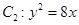 的焦点重合,左端点为
的焦点重合,左端点为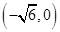
(1)求椭圆的方程;
(2)过椭圆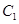 的右焦点且斜率为
的右焦点且斜率为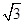 的直线
的直线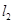 被椭圆
被椭圆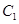 截的弦长
截的弦长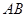 。
。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省福州市高三第五次质量检查数学理卷 题型:选择题
设椭圆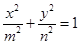 (
(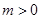 ,
,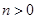 )的右焦点与抛物线
)的右焦点与抛物线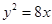 的焦点相同,离心率为
的焦点相同,离心率为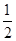 ,则此椭圆的方程为
,则此椭圆的方程为
A.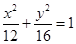 B.
B.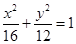 C.
C. D.
D.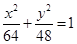
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com