
 解:以巡逻艇所在位置A为原点,走私船在点B的位置,设巡逻艇在C处追上走私船.
解:以巡逻艇所在位置A为原点,走私船在点B的位置,设巡逻艇在C处追上走私船.| BC |
| sin∠BAC |
| AC |
| sin∠ABC |
| 20 |
| 30 |
| ||
| 3 |


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:
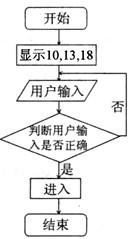 某银行开发出一套网银验证程序,验证规则如下:(1)有两组数字,这两组数字存在一种对应关系;第一组数字a,b,c对应于第二组数字2a+b,c+2b,a+3c;(2)进行验证时程序在电脑屏幕上依次显示产第二组数字,由用户计算出第一组数字后依次输入电脑,只有准确输入方能进入,其流程图如图,试问用户应输入( )
某银行开发出一套网银验证程序,验证规则如下:(1)有两组数字,这两组数字存在一种对应关系;第一组数字a,b,c对应于第二组数字2a+b,c+2b,a+3c;(2)进行验证时程序在电脑屏幕上依次显示产第二组数字,由用户计算出第一组数字后依次输入电脑,只有准确输入方能进入,其流程图如图,试问用户应输入( )| A、3,4,5 | B、4,2,6 | C、2,6,4 | D、3,5,7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2009-2010学年广东省深圳市北大附中南山分校高二(上)期中数学试卷1(理科)(解析版) 题型:解答题
 海里/小时的速度向正北方航行堵截,10分钟后航行到C处,发现海盗船位于北偏西方120°的D处,此时两船相距
海里/小时的速度向正北方航行堵截,10分钟后航行到C处,发现海盗船位于北偏西方120°的D处,此时两船相距 海里,问海盗船每小时行多少海里?
海里,问海盗船每小时行多少海里?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com