
| ���Ŀ�ѧ�� | ��Ȼ��ѧ�� | ���������� | |
| ����� | 4 | 4 | 2 |
| ÿ�ſγ�ѧ�� | 2 | 3 | 1 |
���� ��I�����û����¼��뻥������¼��ĸ��ʼ��㹫ʽ���ɵó���
��II����ѡ�γ̵�ѧ�ֿ���Ϊ��3��3��1������3��2��2�������û����¼��뻥������¼��ĸ��ʼ��㹫ʽ���ɵó���
��III��X�Ŀ���ȡֵΪ4��5��6��7��8��9�����û����¼��뻥������¼��ĸ��ʼ��㹫ʽ���ɵó���
��� �⣺�����������ѡһ������������γ̵��¼�ΪA��$P��A��=\frac{C_2^1C_8^2+C_2^2C_8^1}{{C_{10}^3}}=\frac{8}{15}$��
������ѡһ����Ȼ��ѧ��γ̵��¼�ΪB��$P��B��=\frac{C_4^1C_6^2+C_6^3}{{C_{10}^3}}=\frac{2}{3}$��
���������Ϊ$P��A��B��=P��A��•P��B��=\frac{8}{15}��\frac{2}{3}=\frac{16}{45}$-----------------------��4�֣�
����ѡ�γ̵�ѧ�ֿ���Ϊ��3��3��1������3��2��2����
���Լ�ѡ�γ̵�ѧ������Ϊ7ѧ�ֵĸ���Ϊ$P=\frac{C_4^2C_2^1+C_4^1C_4^2}{{C_{10}^3}}=\frac{3}{10}$-----------------��7�֣�
����X�Ŀ���ȡֵΪ4��5��6��7��8��9----------------------��8�֣�$P��X=4��=\frac{C_2^2C_4^1}{{C_{10}^3}}=\frac{1}{30}$�� $P��X=5��=\frac{C_2^2C_4^1+C_4^2C_2^1}{{C_{10}^3}}=\frac{2}{15}$��$P��X=6��=\frac{C_2^1C_4^1C_4^1+C_4^3}{{C_{10}^3}}=\frac{3}{10}$�� $P��X=7��=\frac{3}{10}$��$P��X=8��=\frac{C_4^2C_4^1}{{C_{10}^3}}=\frac{1}{5}$�� $P��X=9��=\frac{C_4^3}{{C_{10}^3}}=\frac{1}{30}$��
�����������X�ķֲ���Ϊ��
| X | 4 | 5 | 6 | 7 | 8 | 9 |
| P | $\frac{1}{30}$ | $\frac{2}{15}$ | $\frac{3}{10}$ | $\frac{3}{10}$ | $\frac{1}{5}$ | $\frac{1}{30}$ |
���� ���⿼���˻����¼��뻥������¼��ĸ��ʼ��㹫ʽ���������������ѧ�������㹫ʽ��������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
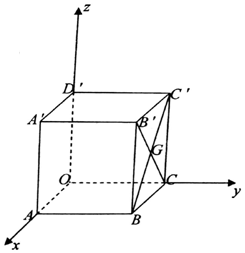 ��ͼ���ⳤΪ1��������OABC-D��A��B��C���У�GΪ����������BCC��B������ģ��Զ���OΪ����ԭ�㽨����ͼ��ʾ�Ŀռ�ֱ������ϵ�����G������Ϊ��$\frac{1}{2}$��1��$\frac{1}{2}$����
��ͼ���ⳤΪ1��������OABC-D��A��B��C���У�GΪ����������BCC��B������ģ��Զ���OΪ����ԭ�㽨����ͼ��ʾ�Ŀռ�ֱ������ϵ�����G������Ϊ��$\frac{1}{2}$��1��$\frac{1}{2}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | -i | D�� | i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ı���ABCD�������Σ�ED��ƽ��ABCD��DE��AF��AF=AD��
��ͼ���ı���ABCD�������Σ�ED��ƽ��ABCD��DE��AF��AF=AD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��a2+b2��0����a��0��b��0�� | B�� | ��a2+b2��0����a��0��b��0�� | ||
| C�� | ��a=0��b=0����a2+b2��0 | D�� | ��a��0��b��0����a2+b2��0 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com