
| 2 |
| 3 |
|
|
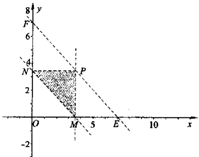 解:(1)设构成三角形的事件为A
解:(1)设构成三角形的事件为A| 2 |
| 4 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 9 |
|
|
|
| S△MNP |
| S△OEF |
| 1 |
| 4 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2012-2013学年河北省邯郸市高三下学期第一次(3月)模拟考试理科数学试卷(解析版) 题型:选择题
把一根长度为7的铁丝截成任意长的3段,则能构成三角形的概率为
A.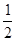 B.
B.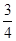 C.
C.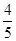 D.
D.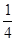
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题12分)
把一根长度为7的铁丝截成3段.
(1)如果三段的长度均为整数,求能构成三角形的概率;
(2)如果把铁丝截成2,2,3的三段放入一个盒子中,然后有放回地摸4次,设摸到长度为2的次数为![]() ,求
,求![]() 与
与![]() ;
;
(3)如果截成任意长度的三段,求能构成三角形的概率.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年浙江省宁波市鄞州高级中学高二(上)期中数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com