
(1)设P点的坐标为(x0,y0),证明![]() <1;
<1;
(2)求四边形ABCD的面积的最小值.
(文)设{an}是等差数列,{bn}是各项都为正数的等比数列,且a1=b1=1,a3+b5=21,a5+b3=13.
(1)求{an}、{bn}的通项公式;
(2)求数列{![]() }的前n项和Sn.
}的前n项和Sn.
答案: (1)证明:椭圆的半焦距c=![]() =1.
=1.
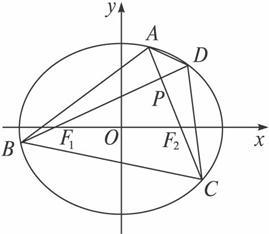
由AC⊥BD知点P在以线段F1F2为直径的圆上,
故x02+y02=1,所以![]() ≤
≤![]() =
=![]() <1.
<1.
(2)解:①当BD的斜率k存在且k≠0时,BD的方程为y=k(x+1),代入椭圆方程![]() =1,
=1,
并化简,得(3k2+2)x2+6k2x+3k2-6=0.设B(x1,y1),D(x2,y2),则x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
|BD|=![]() ·|x1-x2|=
·|x1-x2|=![]() ;
;
因为AC与BD相交于点P,且AC的斜率为-![]() ,所以|AC|=
,所以|AC|=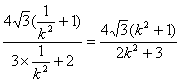 .四边形ABCD的面积为S=
.四边形ABCD的面积为S=![]() ·|BD|·|AC|=
·|BD|·|AC|=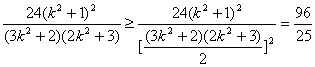 ,
,
当k2=1时,上式取等号.
②当BD的斜率k=0或斜率不存在时,四边形ABCD的面积S=4.综上,四边形ABCD的面积的最小值为![]() .
.
(文)解:(1)设{an}的公差为d,{bn}的公比为q,则依题意有q>0且
解得d=2,q=2.所以an=1+(n-1)d=2n-1,bn=qn-1=2n-1.
(2)![]() =
=![]() .
.
Sn=1+![]() , ①
, ①
2Sn=2+3+![]() +…+
+…+![]() . ②
. ②
②-①,得Sn=2+2+![]() =2+2×(1+
=2+2×(1+![]() +
+![]() )
)![]()
=2+2×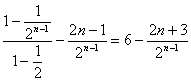 .
.


科目:高中数学 来源: 题型:
A.![]() B.3 C.
B.3 C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
A.3 B.2 C.5 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆![]() +
+![]() =1的左、右焦点分别为F1、F2,点P在椭圆上.若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为( )
=1的左、右焦点分别为F1、F2,点P在椭圆上.若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为( )
A.![]() B.3 C.
B.3 C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源:2013届江西省高二第二次月考文科数学 题型:选择题
已知椭圆 +
+ =1的左、右焦点分别为F1、F2,点P在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为( )
=1的左、右焦点分别为F1、F2,点P在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为( )
A. B.
B. C.
C. 或
或 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com