
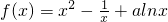 在(1,2)上存在单调递增区间的充要条件是________.
在(1,2)上存在单调递增区间的充要条件是________. ,+∞)
,+∞)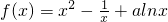 在(1,2)上存在单调递增区间的问题转化为其导函数f′(x)>0在(1,2)上能成立问题,再将导函数的分子看做新函数g(x),通过导数讨论其图象性质即可得g(x)>0在(1,2)上能成立时a的范围
在(1,2)上存在单调递增区间的问题转化为其导函数f′(x)>0在(1,2)上能成立问题,再将导函数的分子看做新函数g(x),通过导数讨论其图象性质即可得g(x)>0在(1,2)上能成立时a的范围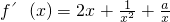 =
= (x>0)
(x>0)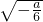 且2>
且2>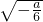 >1
>1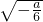 )上是减函数,在(
)上是减函数,在(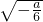 ,2)上为增函数
,2)上为增函数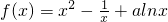 在(1,2)上存在单调递增区间
在(1,2)上存在单调递增区间 ,此时-
,此时- <a<-6
<a<-6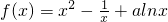 在(1,2)上存在单调递增区间的充要条件是a∈(-
在(1,2)上存在单调递增区间的充要条件是a∈(- ,+∞)
,+∞) ,+∞)
,+∞)

科目:高中数学 来源: 题型:
| f′(x0) |
| ex0 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省佛山一中高二(下)第一次段考数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省德州市乐陵一中高三(上)期末数学复习训练试卷18(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2011年江西省高考数学仿真押题卷07(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2011年江西省高考数学仿真押题卷05(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com