
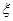 ,求
,求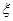 的分布列和数学期望.
的分布列和数学期望. ,
,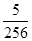 ,
, ;(2)详见解析
;(2)详见解析 ,可依据一等奖、二等奖、三等奖各自的条件求出相应的概率值;
,可依据一等奖、二等奖、三等奖各自的条件求出相应的概率值;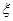 ,则
,则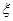 的所有可能取值为1、2、3、4.
的所有可能取值为1、2、3、4. ,不发生的概率则为
,不发生的概率则为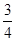 ,根据题意可求
,根据题意可求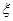 的分布列及数学期望.
的分布列及数学期望.
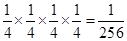 (列式正确,计算错误,扣1分) 2分
(列式正确,计算错误,扣1分) 2分 (列式正确,计算错误,扣1分) 4分
(列式正确,计算错误,扣1分) 4分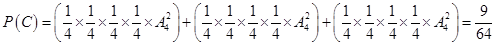 6分
6分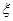 ,则
,则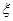 的所有可能取值为1、2、3、4.
的所有可能取值为1、2、3、4.
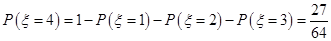 10分
10分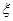 的分布列为:
的分布列为: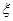 | 1 | 2 | 3 | 4 |
| P |  | 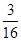 |  |  |
 12分
12分

科目:高中数学 来源:不详 题型:解答题
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 20 | | |
| 乙班 | | 60 | |
| 总计 | | | 210 |
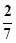 .
.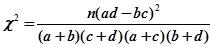 ,其中
,其中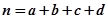 .
.| 参考数据 | 当 ≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; ≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
当 >2.706时,有90%的把握判定变量A,B有关联; >2.706时,有90%的把握判定变量A,B有关联; | |
当 >3.841时,有95%的把握判定变量A,B有关联; >3.841时,有95%的把握判定变量A,B有关联; | |
当 >6.635时,有99%的把握判定变量A,B有关联. >6.635时,有99%的把握判定变量A,B有关联. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,乙获胜的概率为
,乙获胜的概率为 ,则下列说法正确的是( )
,则下列说法正确的是( )A.甲获胜的概率是 | B.甲不输的概率是 |
C.乙输了的概率是 | D.乙不输的概率是 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,该研究性学习小组又分成两个小组进行验证性实验.
,该研究性学习小组又分成两个小组进行验证性实验. 的概率分布列和期望.
的概率分布列和期望. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com