
记者在街上随机抽取10人,在一个月内接到的垃圾短信条数统计的茎叶图如下: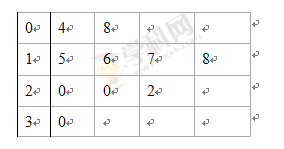
(Ⅰ)计算样本的平均数及方差;
(Ⅱ)现从10人中随机抽出2名,设选出者每月接到的垃圾短信在10条以下的人数为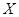 ,求随机变量
,求随机变量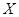 的分布列和期望.
的分布列和期望.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
某校校庆,各届校友纷至沓来,某班共来了n位校友(n>8且n∈N*),其中女校友6位,组委会对这n位校友登记制作了一份校友名单,现随机从中选出2位校友代表,若选出的2位校友是一男一女,则称为“最佳组合”.
(1)若随机选出的2位校友代表为“最佳组合”的概率不小于 ,求n的最大值;
,求n的最大值;
(2)当n=12时,设选出的2位校友代表中女校友人数为ξ,求ξ的分布列和数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
辽宁某大学对参加全运会的志愿者实施“社会教育实践”学分考核,因该批志愿者表现良好,该大学决定考核只有合格和优秀两个等次,若某志愿者考核为合格,授予0.5个学分;考核为优秀,授予1个学分,假设该校志愿者甲、乙、丙考核为优秀的概率分别为 、
、 、
、 ,他们考核所得的等次相互独立.
,他们考核所得的等次相互独立.
(1)求在这次考核中,志愿者甲、乙、丙三人中至少有一名考核为优秀的概率;
(2)记在这次考核中甲、乙、丙三名志愿者所得学分之和为随机变量X,求随机变量X的分布列.
(3)求X的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某班同学利用寒假进行社会实践,对年龄在 的人群随机抽取
的人群随机抽取 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:

(1)补全频率分布直方图,并求 的值;
的值;
(2)从年龄在 的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在
的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
盒子中装有四张大小形状均相同的卡片,卡片上分别标有数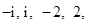 其中
其中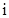 是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).
是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).
(1)求事件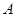 “在一次试验中,得到的数为虚数”的概率
“在一次试验中,得到的数为虚数”的概率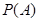 与事件
与事件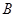 “在四次试验中,
“在四次试验中,
至少有两次得到虚数” 的概率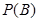 ;
;
(2)在两次试验中,记两次得到的数分别为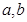 ,求随机变量
,求随机变量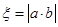 的分布列与数学期望
的分布列与数学期望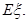
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6, 且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
(1)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(2)记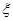 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求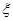 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解某市市民对政府出台楼市限购令的态度,在该市随机抽取了50名市民进行调查,他们月收入(单位:百元)的频数分布及对楼市限购令的赞成人数如下表:
| 月收入 |  | [25,35) | [35,45) |  |  |  |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 8 | 5 | 2 | 1 |
 ,
, <2.706时,没有充分的证据判定赞不赞成楼市限购令与收入高低有关;
<2.706时,没有充分的证据判定赞不赞成楼市限购令与收入高低有关; >2.706时,有90%的把握判定赞不赞成楼市限购令与收入高低有关;
>2.706时,有90%的把握判定赞不赞成楼市限购令与收入高低有关; >3.841时,有95%的把握判定赞不赞成楼市限购令与收入高低有关;
>3.841时,有95%的把握判定赞不赞成楼市限购令与收入高低有关; >6.635时,有99%的把握判定赞不赞成楼市限购令与收入高低有关。
>6.635时,有99%的把握判定赞不赞成楼市限购令与收入高低有关。| | 非高收入族 | 高收入族 | 总计 |
| 赞成 | | | |
| 不赞成 | | | |
| 总计 | | | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知向量
(1)若 分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次正面朝上出现的点数,求满足
分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次正面朝上出现的点数,求满足 的概率.
的概率.
(2)若 在连续区间[1,6]上取值,求满足
在连续区间[1,6]上取值,求满足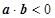 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
小波以游戏方式决定参加学校合唱团还是参加学校排球队.游戏规则为:以O为起点,再从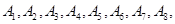 (如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为
(如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为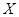 .若
.若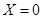 就参加学校合唱团,否则就参加学校排球队.
就参加学校合唱团,否则就参加学校排球队.
(I)求小波参加学校合唱团的概率;
(II)求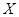 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com