
【题目】【2014课标全国Ⅰ,文12】已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则a的取值范围是( ).
A.(2,+∞) B.(1,+∞)
C.(-∞,-2) D.(-∞,-1)
科目:高中数学 来源: 题型:
【题目】如图,抛物线![]() 的焦点为
的焦点为![]() ,抛物线上一定点
,抛物线上一定点![]() .
.
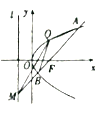
(1)求抛物线![]() 的方程及准线
的方程及准线![]() 的方程;
的方程;
(2)过焦点![]() 的直线(不经过
的直线(不经过![]() 点)与抛物线交于
点)与抛物线交于![]() 两点,与准线
两点,与准线![]() 交于点
交于点![]() ,记
,记![]() 的斜率分别为
的斜率分别为![]() ,问是否存在常数
,问是否存在常数![]() ,使得
,使得![]() 成立?若存在
成立?若存在![]() ,求出
,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
周销售量(单位:吨) | 2 | 3 | 4 |
频数 | 20 | 50 | 30 |
⑴ 根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率;
⑵ 已知每吨该商品的销售利润为2千元,![]() 表示该种商品两周销售利润的和(单位:千元),若以上述频率作为概率,且各周的销售量相互独立,求
表示该种商品两周销售利润的和(单位:千元),若以上述频率作为概率,且各周的销售量相互独立,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中有7个大小、形状相同的小球,6个白球1个红球.现任取1个,若为红球就停止,若为白球就放回,搅拌均匀后再接着取.试设计一个模拟试验,计算恰好第三次摸到红球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.
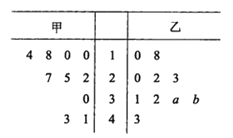
为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)当![]() 时,记甲型号电视机的“星级卖场”数量为
时,记甲型号电视机的“星级卖场”数量为![]() ,乙型号电视机的“星级卖场”数量为
,乙型号电视机的“星级卖场”数量为![]() ,比较
,比较![]() 的大小关系;
的大小关系;
(2)在这10个卖场中,随机选取2个卖场,记![]() 为其中甲型号电视机的“星级卖场”的个数,求
为其中甲型号电视机的“星级卖场”的个数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若![]() ,记乙型号电视机销售量的方差为
,记乙型号电视机销售量的方差为![]() ,根据茎叶图推断
,根据茎叶图推断![]() 为何值时,
为何值时,![]() 达到最小值.(只需写出结论)
达到最小值.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届广西陆川县中学高三文上学期二模】已知函数![]() .
.
(I)求函数![]() 的单调区间;
的单调区间;
(II)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(III)在(II)的条件下,对任意的![]() ,求证:
,求证: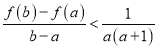 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届安徽百校论坛高三文上学期联考二】已知函数![]() .
.
(1)若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)是否存在整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上存在极小值,若存在,求出所有整数
上存在极小值,若存在,求出所有整数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为集合A,B={x|x<a}.
的定义域为集合A,B={x|x<a}.
(1)求集合A;
(2)若AB,求a的取值范围;
(3)若全集U={x|x≤4},a=-1,求U A及A∩(U B).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com