
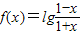 ,有下列三个命题:
,有下列三个命题: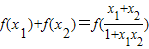 ;
;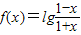 恒有意义,代入计算f(-x)+f(x)可判断①;利用分析法,结合反比例函数及对数函数的单调性和复合函数“同增异减”的原则,可判断②;代入分别计算f(x1)+f(x2)和
恒有意义,代入计算f(-x)+f(x)可判断①;利用分析法,结合反比例函数及对数函数的单调性和复合函数“同增异减”的原则,可判断②;代入分别计算f(x1)+f(x2)和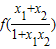 ,比照后可判断③.
,比照后可判断③.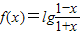 ,当x∈(-1,1)时,
,当x∈(-1,1)时,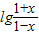 +
+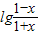 =
=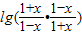 =lg1=0,故f(-x)=-f(x),即①正确;
=lg1=0,故f(-x)=-f(x),即①正确;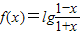 =
=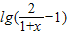 ,由y=
,由y=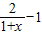 在(-1,1)上是减函数,故f(x)在(-1,1)上是减函数,即②正确;
在(-1,1)上是减函数,故f(x)在(-1,1)上是减函数,即②正确;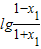 +
+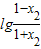 =
= =
=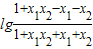 ;
;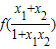 =
=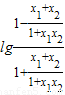 =
= ,即③正确
,即③正确

科目:高中数学 来源:2007-2008学年山东省聊城市高三(上)期中数学试卷(文科)(解析版) 题型:选择题
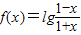 ,有下列三个命题:
,有下列三个命题: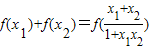 ;
;查看答案和解析>>
科目:高中数学 来源:2010-2011学年黑龙江省大庆实验中学高二(上)开学数学试卷(理科)(解析版) 题型:填空题
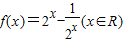 .有下列三个结论:①f(x)的值域为R;②f(x)是R上的增函数;③f(x)的图象是中心对称图形,其中所有正确命题的序号是 .
.有下列三个结论:①f(x)的值域为R;②f(x)是R上的增函数;③f(x)的图象是中心对称图形,其中所有正确命题的序号是 .查看答案和解析>>
科目:高中数学 来源:2010-2011学年黑龙江省大庆实验中学高一(下)开学数学试卷(解析版) 题型:填空题
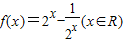 .有下列三个结论:①f(x)的值域为R;②f(x)是R上的增函数;③f(x)的图象是中心对称图形,其中所有正确命题的序号是 .
.有下列三个结论:①f(x)的值域为R;②f(x)是R上的增函数;③f(x)的图象是中心对称图形,其中所有正确命题的序号是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com