
已知抛物线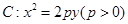 ,直线
,直线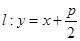 交抛物线于
交抛物线于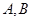 两点,且
两点,且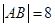 .
.
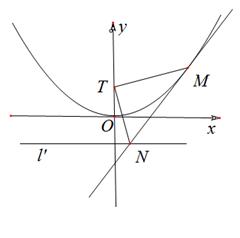
(1)求抛物线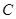 的方程;
的方程;
(2)若点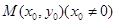 是抛物线
是抛物线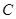 上的动点,过
上的动点,过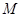 点的抛物线的切线与直线
点的抛物线的切线与直线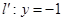 交于点
交于点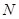 ,问在
,问在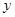 轴上是否存在定点
轴上是否存在定点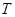 ,使得
,使得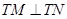 ?若存在,求出该定点,并求出
?若存在,求出该定点,并求出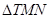 的面积的最小值;若不存在,请说明理由.
的面积的最小值;若不存在,请说明理由.
(1)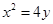 .(2)存在定点(0,1),
.(2)存在定点(0,1),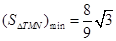 .
.
【解析】
试题分析:(1)把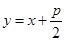 代入
代入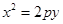 ,消去
,消去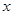 ,整理得
,整理得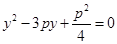 ,
,
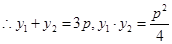 2分
2分
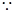
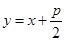 过抛物线的焦点
过抛物线的焦点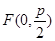 ,
,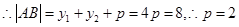
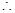 抛物线
抛物线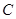 的方程为
的方程为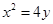 .
6分
.
6分
(2)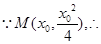 切线方程为
切线方程为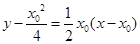 ,即
,即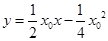 ,
,
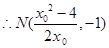 8分
8分
令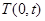 ,
,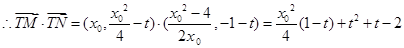 ,
,
当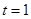 时,
时,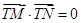 ,即
,即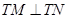 ,
,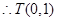 10分
10分
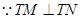 ,
,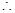
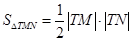 ,
,
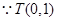 点是抛物线的焦点,
点是抛物线的焦点,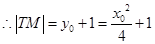 ,
,
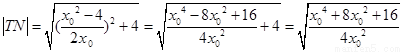
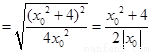 ,
,
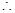
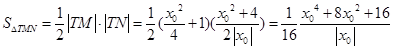 ,
13分
,
13分
不妨设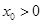 ,令
,令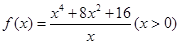 ,
,
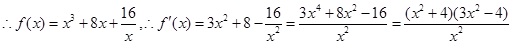 ,
,
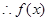 在
在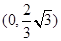 上递减,在
上递减,在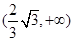 上递增,
上递增,
 ,
,
即当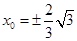 时,
时,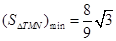 . 15分
. 15分
考点:本题考查了直线与抛物线的综合运用
点评:解决抛物线中的定值及最值问题的基本思想是建立目标函数和建立不等式(方程)关系,根据条件求解定值及最值,因此这里问题的难点就是如何建立目标函数和不等式(或等量关系)。建立目标函数的关键是选用一个合适变量,这个变量可以是直线的斜率、直线的截距、点的坐标等,要根据实际情况灵活处理。


科目:高中数学 来源: 题型:
| 2m |
| 3 |
| x2 |
| 4m2 |
| y2 |
| 3m2 |
| 2m |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分18分)第一题满分4分,第二题满分6分,第三题满分8分.
已知椭圆![]() 的长轴长是焦距的两倍,其左、右焦点依次为
的长轴长是焦距的两倍,其左、右焦点依次为![]() 、
、![]() ,抛物线
,抛物线![]()
![]() 的准线与
的准线与![]() 轴交于
轴交于![]() ,椭圆
,椭圆![]() 与抛物线
与抛物线![]() 的一个交点为
的一个交点为![]() .
.
(1)当![]() 时,求椭圆
时,求椭圆![]() 的方程;
的方程;
(2)在(1)的条件下,直线![]() 过焦点
过焦点![]() ,与抛物线
,与抛物线![]() 交于
交于![]() 两点,若弦长
两点,若弦长![]() 等于
等于![]() 的周长,求直线
的周长,求直线![]() 的方程;
的方程;
(3)由抛物线弧![]()
![]() 和椭圆弧
和椭圆弧![]()
![]()
(![]() )合成的曲线叫“抛椭圆”,是否存在以原点
)合成的曲线叫“抛椭圆”,是否存在以原点![]() 为直角顶点,另两个顶点
为直角顶点,另两个顶点![]() 落在“抛椭圆”上的等腰直角三角形
落在“抛椭圆”上的等腰直角三角形![]() ,若存在,求出两直角边所在直线的斜率;若不存在,说明理由.
,若存在,求出两直角边所在直线的斜率;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2011年上海市浦东新区高考数学三模试卷(理科)(解析版) 题型:解答题
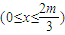 和椭圆弧
和椭圆弧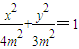

查看答案和解析>>
科目:高中数学 来源:2011年上海市浦东新区高考数学三模试卷(理科)(解析版) 题型:解答题
 和椭圆弧
和椭圆弧

查看答案和解析>>
科目:高中数学 来源: 题型:
如图,已知抛物线方程为![]() .
.
⑴直线![]() 过抛物线的焦点F,且垂直于x轴,
过抛物线的焦点F,且垂直于x轴,![]() 与抛物线交于
与抛物线交于
A、B两点,求AB的长度.
⑵直线![]() 过抛物线的焦点
过抛物线的焦点![]() ,且倾斜角为
,且倾斜角为![]() ,直线
,直线![]() 与抛
与抛
物线相交于C、D两点,O为原点.求△OCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com