
【题目】已知f(x),g(x)都是定义在R上的函数,并满足:
1)f(x)=2axg(x),(a>0,a≠1);
2)g(x)≠0;
3)f(x)g′(x)<f′(x)g(x)且 ![]() +
+ ![]() =5,则a= .
=5,则a= .
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】有甲、乙两个班级进行数学考试,按照大于或等于90分为优秀,90分以下为非优秀统计成绩后,得到如表的列联表.
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 100 |
已知在全部100人中抽到随机抽取1人为优秀的概率为 ![]() .
.
(1)请完成如表的列联表;
(2)根据列联表的数据,有多大的把握认为“成绩与班级有关系“?
(3)按分层抽样的方法,从优秀学生中抽出6名组成一个样本,再从样本中抽出2名学生,求恰好有1个学生在甲班的概率.
参考公式和数据:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
下面的临界值表供参考:
p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一生物科研小组对升高温度的多少与某种细菌种群存活数量之间的关系进行分析研究,他们制作5 份相同的样本并编号1、2、3、4、5,分别记录它们同在![]() 下升高不同的温度后的种群存活数量, 得到如下资料:
下升高不同的温度后的种群存活数量, 得到如下资料:
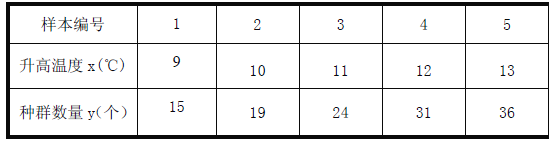
(1)若随机选取2份样本的数据来研究,求其编号不相邻的概率;
(2)求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(3)利用(2)中所求出的回归方程预测温度升高15 ![]() 时此种样本中种菌群存活数量.
时此种样本中种菌群存活数量.
附: 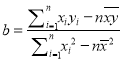 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3﹣
x3﹣ ![]() (a∈R).
(a∈R).
(1)若a=1,求函数f(x)在[0,2]上的最大值;
(2)若对任意x∈(0,+∞),有f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有垣厚五尺,两鼠对穿.大鼠日一尺,小鼠亦日一尺.大鼠日自倍,小鼠日自半.问几何日相逢?各穿几何?”,翻译成今天的话是:一只大鼠和一只小鼠分别从的墙两侧面对面打洞,已知第一天两鼠都打了一尺长的洞,以后大鼠每天打的洞长是前一天的2倍,小鼠每天打的洞长是前一天的一半,已知墙厚五尺,问两鼠几天后相见?相见时各打了几尺长的洞?设两鼠x 天后相遇(假设两鼠每天的速度是匀速的),则x=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点M(﹣ ![]() ),N是圆C:(x﹣
),N是圆C:(x﹣ ![]() )2+y2=16(C为圆心) 上的动点,MN的垂直平分线与NC交于点E.
)2+y2=16(C为圆心) 上的动点,MN的垂直平分线与NC交于点E.
(1)求动点E的轨迹方程C1;
(2)直线l与轨迹C1交于P,Q两点,与抛物线C2:x2=4y交于A,B两点,且抛物线C2在点A,B处的切线垂直相交于S,设点S到直线l的距离为d,试问:是否存在直线l,使得d= ![]() ?若存在,求直线l的方程;若不存在,请说明理由.
?若存在,求直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视传媒公司为了解某地区电视观众对里约奥运会的收视情况,随机抽取了100名观众进行调查,其中女性有55名,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
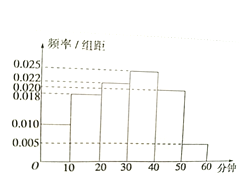
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”。已知“体育迷”中有10名女性。
(1)试求“体育迷”中的男性观众人数;
(2)据此资料完成![]() 列联表,你是否认为“体育迷”与性别有关?
列联表,你是否认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | |||
合计 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
临界值表供参考参考公式:
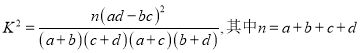
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若椭圆C1: ![]() 的离心率等于
的离心率等于 ![]() ,抛物线C2:x2=2py(p>0)的焦点在椭圆C1的顶点上.
,抛物线C2:x2=2py(p>0)的焦点在椭圆C1的顶点上.
(1)求抛物线C2的方程;
(2)求过点M(﹣1,0)的直线l与抛物线C2交E、F两点,又过E、F作抛物线C2的切线l1、l2 , 当l1⊥l2时,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com