
如图8所示,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的 倍,点P在侧棱SD上,且
倍,点P在侧棱SD上,且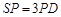 .
.
(Ⅰ)求证:AC⊥SD;
(Ⅱ)求二面角P-AC-D的大小;
(Ⅲ)侧棱SC上是否存在一点E,使得BE∥平面PAC.若存在,求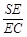 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.
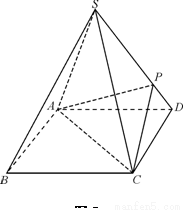
(Ⅰ)连接BD,设AC交BD于O,
由题意SO⊥AC.在正方形ABCD中,AC⊥BD,
∴AC⊥平面SBD,又SDÌ平面SBD,
∴AC⊥SD.··················· 4分
(Ⅱ)设正方形ABCD的边长为a,则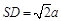 ,又
,又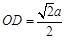 ,
,
∴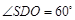 ,由(Ⅰ)知AC⊥平面SBD,又OPÌ平面SBD,
,由(Ⅰ)知AC⊥平面SBD,又OPÌ平面SBD,
∴AC⊥OP,且AC⊥OD,
∴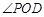 是二面角P-AC-D的平面角.
是二面角P-AC-D的平面角.
△POD中,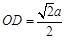 ,
,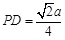 ,
,
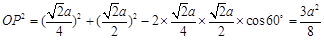 ,则
,则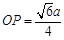 ,
,
∴△POD是Rt△,又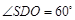 ,∴
,∴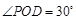 .
.
即二面角P-AC-D的大小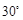 .···················· 9分
.···················· 9分
(Ⅲ)在棱SC上存在一点E,使得BE∥平面PAC.
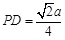 ,在SP上取一点N,使
,在SP上取一点N,使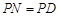 ,过N作PC的平行线与SC的交点即为E,连结BN、BE.
,过N作PC的平行线与SC的交点即为E,连结BN、BE.
在△BND中,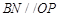 ,又
,又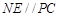 ,
,
∴平面BEN∥平面PAC,又BEÌ平面BEN,
∴BE∥平面PAC,由于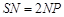 ,故
,故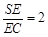
【解析】略


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com