
 ,点P到平面α的距离PH=0.4(km)。沿山脚原有一段笔直的公路AB可供利用,从点O到山脚修路的造价为a万元/km,原有公路改建费用为
,点P到平面α的距离PH=0.4(km)。沿山脚原有一段笔直的公路AB可供利用,从点O到山脚修路的造价为a万元/km,原有公路改建费用为 万元/km。当山坡上公路长度为lkm(1≤l≤2)时,其造价为(l2+1)a万元。已知OA⊥AB,PB⊥AB,AB=1.5(km),OA=
万元/km。当山坡上公路长度为lkm(1≤l≤2)时,其造价为(l2+1)a万元。已知OA⊥AB,PB⊥AB,AB=1.5(km),OA= (km),
(km),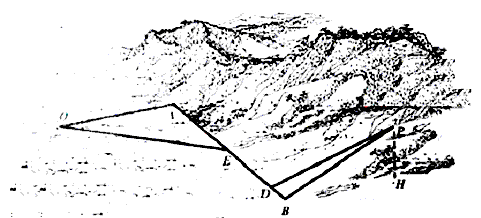
解:(I)如图,PH⊥α,HB ,PB⊥AB, ,PB⊥AB,由三垂线定理逆定理知,AB⊥HB, 所以∠PBH是山坡面与α所成二面角的平面角, 则∠PBH=  , ,设BD=x(km),0≤x≤1.5, 则  , ,记总造价为  万元, 万元,据题设有    , ,当  (km)时总造价 (km)时总造价 最小。 最小。 |
 |
(Ⅱ)设AE=y(km),0≤y≤ ,总造价为 ,总造价为 万元, 万元,根据题设有   , ,则  , ,由  ,得y=1, ,得y=1,当y∈(0,1)时,  在(0,1)内是减函数; 在(0,1)内是减函数;当  内是增函数; 内是增函数;故当y=1,即AE=1(km)时总造价  最小, 最小,且最小总造价为  万元。 万元。(Ⅲ)不存在这样的点D′、E′。 事实上,在AB上任取不同的两点D′、E′。 为使总造价最小,E′显然不能位于D′与B之间, 故可设E′位于D′与A之间, 且  ,0≤x1+y1≤ ,0≤x1+y1≤ , ,总造价为S万元, 则  , ,类似于(I)、(II)的讨论知,  , ,当且仅当  同时成立时, 同时成立时,上述两个不等式等号同时成立, 此时  (km),AE′=1(km),S取得最小值 (km),AE′=1(km),S取得最小值 , ,点D′、E′分别与点D、E重合; 所以不存在这样的点D′、E′,使沿折线PD′E′O修建公路的总造价小于(II)中得到的最小总造价。 |


科目:高中数学 来源:0103 月考题 题型:解答题
 SB=
SB= SC,O为BC的中点。
SC,O为BC的中点。 
查看答案和解析>>
科目:高中数学 来源:0103 期末题 题型:解答题
 的值为多少时能使D1M⊥平面EFB1?试给出证明。
的值为多少时能使D1M⊥平面EFB1?试给出证明。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.圆内接四边形 | B.矩形 |
| C.圆外切四边形 | D.平行四边形 |
查看答案和解析>>
科目:高中数学 来源:高考真题 题型:解答题
 ,AB=AC。
,AB=AC。
查看答案和解析>>
科目:高中数学 来源:浙江省期中题 题型:填空题

查看答案和解析>>
科目:高中数学 来源:浙江 题型:单选题
| A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β |
| B.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β |
| C.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ |
| D.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com