Question

（08年师大附中）已知：三棱柱ABC－A₁B₁C₁中，各棱长均为2，平面ABC⊥平面AA₁C₁C，

∠A₁AC＝60°．

（1）求证：B₁C⊥平面A₁BC₁；

（2）求二面角B₁－A₁B－C₁的大小；

  （3）设O是线段A₁C的中点，P是△ABC内部及边界上的一动点，使OP//平面A₁BC₁，试指出动点P的轨迹图形是什么？请说明你的理由.

 

Answer 1

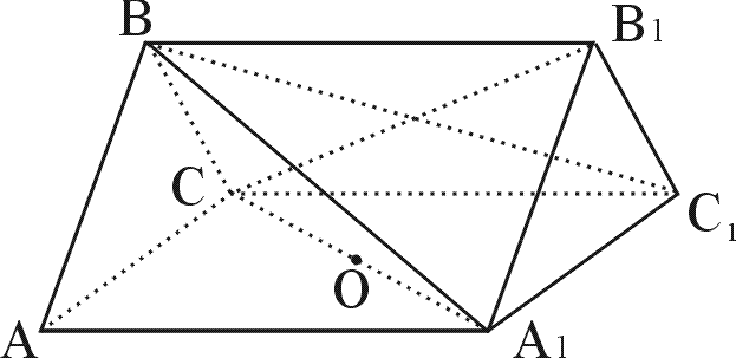
解析：（1）证明：取A₁C₁的中点M，连CM、B₁M

∵三棱柱ABC－A₁B₁C₁　　∴各棱长均相等，∠A₁AC＝60°

∴△A₁CC₁与△A₁B₁C₁都是等边三角形

∴

∵平面ABC⊥平面AA₁C₁C，　

∴平面A₁B₁C₁⊥平面AA₁C₁C

∴B₁M⊥平面AA₁C₁C，由三垂线定理得：B₁C⊥A₁C₁

又∵四边形BCC₁B₁是菱形，∴B₁C⊥BC₁　　

而

∴B₁C⊥平面A₁BC₁

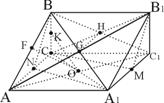
（2）连AB₁与A₁B交于G点，设B₁C与BC₁交于H点，连GH，则GH

取AC的中点N，连BN，A₁N，可证AC⊥A₁B　　∴GH⊥A₁B

又∵四边形AA₁B₁B是菱形　　∴AB₁⊥A₁B

∴∠B₁GH就是所求二面角的平面角

由（1）知A₁C₁⊥B₁C　　∴GH⊥B₁C

设A₁C₁＝a，则

∴即所求二面角的大小为

（3）取AB的中点F，BC的中点K，连OF，OK，连AC₁必过O点，且O为AC₁的中点，则OF//BC₁　　　∴OF//平面A₁BC₁　　∵

∴平面OFK//平面A₁BC₁

在线段FK上（含端点）任取一点P，连OP，则OP//平面A₁BC₁

而过平面A₁BC₁外一点O只能作出一个平面与其平行

因此，点P的轨迹就是线段FK

法二：取AC的中点E，连BE，EA₁

∵三棱柱ABC－A₁B₁C₁的各棱长相等，且∠A₁AC＝60°

∴△ABC与△AA₁C为正三角形

∴BE⊥AC，A₁E⊥AC

∵平面ABC⊥平面AA₁C₁C

∴BE⊥平面AA₁C₁C

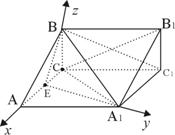
以E为坐标原点，EA为x轴，EA₁为y轴，EB为z轴，建立如右图所示的空间坐标系，设AB＝2

则

（1）∵

又

∴且

∴平面

（2）设是平面AA₁B的法向量

则取

同理可求平面A₁BC₁的法向量

∴

即所求的二面角的大小为