
【题目】已知两个正数a,b,可按规则![]() 扩充为一个新数c,在a,b,c三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.
扩充为一个新数c,在a,b,c三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.
(1)若a=1,b=3,按上述规则操作三次,扩充所得的数是_____________;
(2)若p>q>0,经过6次操作后扩充所得的数为![]() (m,n为正整数),
(m,n为正整数),
则m,n的值分别为____________.
【答案】 255 8,13
【解析】(1)a=1,b=3,按规则操作三次,
第一次:c=ab+a+b=1×3+1+3=7
第二次,7>3>1所以有:c=3×7+3+7=31
第三次:31>7>3所以有:c=7×31+7+31=255
2、p>q>0第一次得:c1=pq+p+q=(q+1)(p+1)1
因为c>p>q,所以第二次得:c2=(c1+1)(p+1)1=(pq+p+q)p+p+(pq+p+q)=(p+1)2(q+1)1
所得新数大于任意旧数,所以第三次可得c3=(c2+1)(c1+1)1=(p+1)3(q+1)21
第四次可得:c4=(c3+1)(c21)1=(p+1)5(q+1)31
故经过6次扩充,所得数为:(q+1)8(p+1)131
∴m=8,n=13
故答案为:255;8,13


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=x![]() (m∈N*).
(m∈N*).
(1)试确定该函数的定义域,并指明该函数在其定义域上的单调性;
(2)若该函数还经过点(2, ![]() ),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.
),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在区间
是定义在区间![]() 上的奇函数,且
上的奇函数,且![]() 若对于任意的
若对于任意的![]() 有
有![]()
(1)判断并证明函数的单调性;
(2)解不等式![]() ;
;
(3)若![]() 对于任意的
对于任意的![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是(-∞,+∞)上的奇函数,且f(x)的图象关于x=1对称,当x∈[0,1]时,f(x)=2x-1.
(1)当x∈[1,2]时,求f(x)的解析式;
(2)计算f(0)+f(1)+f(2)+…+f(2017)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
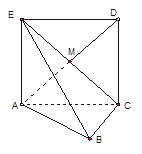
【题目】如图,边长为2的正方形ACDE所在的平面与平面ABC垂直,AD与CE的交点为M,![]() ,且AC=BC.
,且AC=BC.
(1)求证:![]() 平面EBC;
平面EBC;
(2)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线L的参数方程为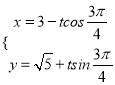 (
(![]() 为参数).在以原点
为参数).在以原点 ![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标中,圆C的方程为
轴正半轴为极轴的极坐标中,圆C的方程为![]() .
.
(Ⅰ)写出直线L的倾斜角![]() 和圆C的直角坐标方程;
和圆C的直角坐标方程;
(Ⅱ)若点 P坐标为![]() ,圆C与直线L交于 A,B两点,求|PA|
,圆C与直线L交于 A,B两点,求|PA|![]() |PB|的值.
|PB|的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届广东省珠海市高三上学期期末考试文数】已知函数![]() 的最小值为0,其中
的最小值为0,其中![]() ,设
,设![]() .
.
(1)求![]() 的值;
的值;
(2)对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)讨论方程![]() 在
在![]() 上根的个数.
上根的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com