
若点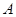 的坐标为
的坐标为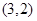 ,
,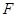 是抛物线
是抛物线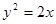 的焦点,点
的焦点,点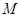 在抛物线上移动时,使
在抛物线上移动时,使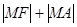 取得最小值的
取得最小值的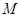 的坐标为( )
的坐标为( )
A.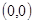 B.
B.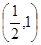 C.
C.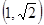 D.
D.
D
【解析】
试题分析:求出焦点坐标和准线方程,把|MF|+|MA|转化为|MA|+|PM|,利用 当P、A、M三点共线时,|MA|+|PM|取得最小值,把y=2代入抛物线y2="2x"
解得x值,即得M的坐标.解:由题意得 F(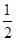 ,0),准线方程为 x=-
,0),准线方程为 x=-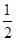 ,设点M到准线的距离为d=|PM|,则由抛物线的定义得|MA|+|MF|=|MA|+|PM|,故当P、A、M三点共线时,|MF|+|MA|取得最小值为|AP|=3-(-
,设点M到准线的距离为d=|PM|,则由抛物线的定义得|MA|+|MF|=|MA|+|PM|,故当P、A、M三点共线时,|MF|+|MA|取得最小值为|AP|=3-(-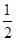 )=
)=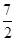 .把 y=2代入抛物线y2="2x" 得 x=2,故点M的坐标是(2,2),故选D.
.把 y=2代入抛物线y2="2x" 得 x=2,故点M的坐标是(2,2),故选D.
考点:抛物线的定义和性质
点评:本题考查抛物线的定义和性质得应用,解答的关键利用是抛物线定义,体现了转化的数学思想


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
| FP1 |
| FP2 |
| FP3 |
| FP1 |
| FP2 |
| FPn |
| 0 |
| FP1 |
| FP2 |
| FPn |
| FP1 |
| FP2 |
| FPN |
| FP1 |
| FP2 |
| FPN |
| 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ;
; ,求证:
,求证: ;
; ,则
,则 ”开展了研究并发现其为假命题.
”开展了研究并发现其为假命题.查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆![]() 是抛物
是抛物
线![]() 的一条切线.
的一条切线.
(I)求椭圆的方程;
(II)过点![]() 的动直线L交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T?若存在,求出点T的坐标;若不存在,请说明理由.
的动直线L交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T?若存在,求出点T的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2012年上海市普陀区高考数学一模试卷(理科)(解析版) 题型:解答题
 ;
; ,求证:
,求证: ;
; ,则
,则 ”开展了研究并发现其为假命题.
”开展了研究并发现其为假命题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com