
分析 (1)利用数列递推式,代入计算可得结论;
(2)利用(1)的结论,猜想an的表达式,再用数学归纳法证明.
解答 解:(1)由已知得${S_n}=\frac{{n{a_n}+na}}{2}=\frac{{{a_n}+a}}{2}•n$,
当n=1时,${a_1}={S_1}=\frac{{{a_1}+a}}{2}$,则a1=a,${S_3}={a_1}+{a_2}+{a_3}=\frac{{{a_3}+a}}{2}•3$,而a2=a+2,
于是可解得a3=a+4;同理可解得a4=a+6.
(2)由(1)中的a1=a,a2=a+2,a3=a+4,a4=a+6,…,
猜测出an=a+2(n-1).
数学归纳法证明如下:
①当n=1时,a1=a=a+2(1-1),猜想成立;
当n=2时,a2=a+2=a+2(2-1),猜想也成立.
②假设当n=k(k∈N*,k≥2)时猜想成立,即ak=a+2(k-1),
则当n=k+1时,${a_{k+1}}={S_{k+1}}-{S_k}=\frac{{{a_{k+1}}+a}}{2}•(k+1)-$$\frac{{{a_k}+a}}{2}•k$,
即(k-1)ak+1=kak-a,
由k≥2可得${a_{k+1}}=\frac{{k{a_k}-a}}{k-1}=\frac{ka+2k(k-1)-a}{k-1}$,
即ak+1=a+2k=a+2[(k+1)-1],
也就是说,当n=k+1时猜想也成立.
由①、②可知对任意的n∈N*,an=a+2(n-1)都成立.
点评 本题考查数列递推式,考查数列的通项,考查数学归纳法,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,1]∪[2,+∞) | B. | [1,2] | C. | [0,1] | D. | [-1,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | c<a<b | C. | b<a<c | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
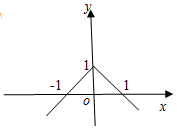
| A. | f(x)=-|x|-1 | B. | f(x)=|x-1| | C. | f(x)=-|x|+1 | D. | f(x)=|x+1| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com