
【题目】已知以点C(t, ![]() )(t∈R,t≠0)为圆心的圆过原点O.
)(t∈R,t≠0)为圆心的圆过原点O.
(1)设直线3x+y﹣4=0与圆C交于点M、N,若|OM|=|ON|,求圆C的方程;
(2)在(1)的条件下,设B(0,2),且P、Q分别是直线l:x+y+2=0和圆C上的动点,求|PQ|﹣|PB|的最大值及此时点P的坐标.
【答案】
(1)解:∵OM=ON,所以,则原点O在MN的中垂线上.
设MN的中点为H,则CH⊥MN,
∴C、H、O三点共线,
∵直线MN的方程是3x+y﹣4=0,
∴直线OC的斜率 ![]() =
= ![]() =
= ![]() ,解得t=3或t=﹣3,
,解得t=3或t=﹣3,
∴圆心为C(3,1)或C(﹣3,﹣1)
∴圆C的方程为(x﹣3)2+(y﹣1)2=10或(x+3)2+(y+1)2=10
由于当圆方程为(x+3)2+(y+1)2=10时,圆心到直线3x+y﹣4=0的距离d>r,
此时不满足直线与圆相交,故舍去,
∴圆C的方程为(x﹣3)2+(y﹣1)2=10
(2)解:在三角形PBQ中,两边之差小于第三边,故|PQ|﹣|PB|≤|BQ|
又B,C,Q三点共线时|BQ|最大
所以,|PQ|﹣|PB|的最大值为 ![]() ,
,
∵B(0,2),C(3,1),∴直线BC的方程为 ![]() ,
,
∴直线BC与直线x+y+2=0的交点P的坐标为(﹣6,4)
【解析】(1)由OM=ON得原点O在MN的中垂线上,由圆的弦中点性质和直线垂直的条件列出方程,求出t的值和C的坐标,代入圆的标准方程化简,再验证直线与圆的位置关系;(2)根据三边关系判断出取最大值的条件,由圆外一点与圆上一点距离最值问题求出最大值,由点斜式方程求出BC的直线方程,以及此时点P的坐标.


科目:高中数学 来源: 题型:
【题目】【2017河北唐山二模】某仪器经过检验合格才能出厂,初检合格率为![]() :若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为
:若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为![]() .每台仪器各项费用如表:
.每台仪器各项费用如表:
项目 | 生产成本 | 检验费/次 | 调试费 | 出厂价 |
金额(元) | 1000 | 100 | 200 | 3000 |
(Ⅰ)求每台仪器能出厂的概率;
(Ⅱ)求生产一台仪器所获得的利润为1600元的概率(注:利润![]() 出厂价
出厂价![]() 生产成本
生产成本![]() 检验费
检验费![]() 调试费);
调试费);
(Ⅲ)假设每台仪器是否合格相互独立,记![]() 为生产两台仪器所获得的利润,求
为生产两台仪器所获得的利润,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017镇江一模20】已知函数![]() ,
,![]() (
(![]() 为常数).
为常数).
(1)若函数![]() 与函数
与函数![]() 在
在![]() 处有相同的切线,求实数
处有相同的切线,求实数![]() 的值;
的值;
(2)若![]() ,且
,且![]() ,证明:
,证明:![]() ;
;
(3)若对任意![]() ,不等式恒
,不等式恒![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数h(x)=2sin(2x+ ![]() )的图象向右平移
)的图象向右平移 ![]() 个单位,再向上平移2个单位,得到函数f(x)的图象,则函数f(x)的图象( )
个单位,再向上平移2个单位,得到函数f(x)的图象,则函数f(x)的图象( )
A.关于直线x=0对称
B.关于直线x=π对称
C.关于点( ![]() ,0)对称
,0)对称
D.关于点( ![]() ,2)对称
,2)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017年第二次全国大联考江苏卷】若无穷数列![]() 满足:
满足:![]() 恒等于常数
恒等于常数![]() ,则称
,则称![]() 具有局部等差数列
具有局部等差数列![]() .
.
(1)若![]() 具有局部等差数列
具有局部等差数列![]() ,且
,且![]()
![]() ,求
,求![]() ;
;
(2)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是公比为正数的等比数列,
是公比为正数的等比数列,![]() ,
,![]() ,
,![]() ,判断
,判断![]() 是否具有局部等差数列
是否具有局部等差数列![]() ,并说明理由;
,并说明理由;
(3)设![]() 既具有局部等差数列
既具有局部等差数列![]() ,又具有局部等差数列
,又具有局部等差数列![]() ,求证:
,求证:![]() 具有局部等差数列
具有局部等差数列![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2016-2017学年度苏锡常镇四市高三教学情况调研(二)】某科研小组研究发现:一棵水蜜桃树的产量![]() (单位:百千克)与肥料费用
(单位:百千克)与肥料费用![]() (单位:百元)满足如下关系:
(单位:百元)满足如下关系:![]() ,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)
,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)![]() 百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为
百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为![]() (单位:百元).
(单位:百元).
(1)求利润函数![]() 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(2)当投入的肥料费用为多少时,该水蜜桃树获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 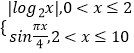 .
.
(1)设函数g(x)=f(x)﹣1,求函数g(x)的零点;
(2)若函数f(x1)=f(x2)=f(x3)=f(x4),且0<x1<x2<x3<x4≤10,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com