
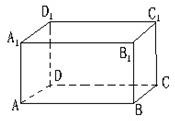
 已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )
已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )A、
| ||
B、5
| ||
C、4
| ||
D、3
|
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源: 题型:
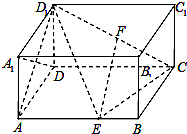 已知如图,在长方体ABCD-A1B1C1D1中,AB=2BC=2AA1=2,点E在棱AB上移动,点F为CD1的中点.
已知如图,在长方体ABCD-A1B1C1D1中,AB=2BC=2AA1=2,点E在棱AB上移动,点F为CD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在长方体ABCD-A1B1C1D1中,已知BC=AA1=1,AB=2,P是A1B1的中点,则直线PB与平面BB1D1D所成角的大小为
如图所示,在长方体ABCD-A1B1C1D1中,已知BC=AA1=1,AB=2,P是A1B1的中点,则直线PB与平面BB1D1D所成角的大小为
| ||
| 10 |
| ||
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
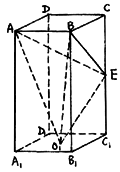
已知:如图,长方体ABCD—![]() 中,AB=BC=4,
中,AB=BC=4,![]() ,E为
,E为![]() 的中点,
的中点,![]() 为下底面正方形的中心.求:(I)二面角C—AB—
为下底面正方形的中心.求:(I)二面角C—AB—![]() 的正切值;
的正切值;
(II)异面直线AB与![]() 所成角的正切值;
所成角的正切值;
(III)三棱锥![]() ——ABE的体积.
——ABE的体积.
 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省连云港市高一(上)期末数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com