
对于任意实数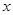 ,<
,<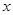 >表示不小于
>表示不小于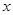 的最小整数,例如<1.1>=2,<
的最小整数,例如<1.1>=2,<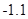 >=
>= 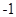 ,那么“
,那么“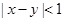 ”是“<
”是“<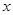 >=<
>=<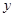 >”( ).
>”( ).
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
B
【解析】
试题分析:若|x-y|<1.取x=3.6,y=4.1,则<x>=4,<y>=5,<x>≠<y>,所以“|x-y|<1”成立推不出“<x>=<y>”成立,若<x>=<y>,因为<x>表示不小于x的最小整数,所以x≤<x><x+1,所以可设<x>=x+m,<y>=y+n,mn∈[0,1],由x+m=y+n得|x-y|=|m-n|<1,所以“<x>=<y>”?“|x-y|<1”
故“|x-y|<1”是“<x>=<y>”的必要不充分条件,故选B
考点:本题考查了充要条件的判断
点评:说明一个命题不成立常用举反例的方法、考查利用充要条件的定义判断一个命题是另一个命题的什么条件.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源:2012届河南省卢氏一高高三适应性考试理科数学 题型:解答题
(本小题满分12分)设函数f(x)的定义域是R,对于任意实数m,n,恒有f(m+n)=f(m)f(n),且当x>0时,0<f(x)<1。
(1)求证:f(0)=1,且当x<0时,有f(x)>1;
(2)判断f(x)在R上的单调性;
⑶设集合A={(x,y)|f(x2)f(y2)>f(1)},集合B={(x,y)|f(ax-y+2)=1,a∈R},若A∩B= ,求a的取值范围。
,求a的取值范围。
查看答案和解析>>
科目:高中数学 来源:2014届福建省高二下学期5月月考文科数学卷(解析版) 题型:选择题
如果函数f(x)=x +bx+c对于任意实数t,都有f(2+t)=f(2-t),那么( )
+bx+c对于任意实数t,都有f(2+t)=f(2-t),那么( )
A.f(2)<f(1)<f(4) B.f(1)<f(2)<f(4)
C.f(2)<f(4)<f(1) D.f(4)<f(2)<f(1)
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三下学期模拟冲刺考试理科数学试卷(解析版) 题型:填空题
如果对于任意实数a,b(a<b),随机变量X满足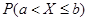 =
=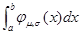 ,称随机变量X服从正态分布,记为
,称随机变量X服从正态分布,记为 ,若X~(0,1),P(X>1)=p,则
,若X~(0,1),P(X>1)=p,则 =________
=________
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省卢氏一高高三适应性考试理科数学 题型:解答题
(本小题满分12分) 设函数f(x)的定义域是R,对于任意实数m,n,恒有f(m+n)=f(m)f(n),且当x>0时,0<f(x)<1。
(1)求证:f(0)=1,且当x<0时,有f(x)>1;
(2)判断f(x)在R上的单调性;
⑶设集合A={(x,y)|f(x2)f(y2)>f(1)},集合B={(x,y)|f(ax-y+2)=1,a∈R},若A∩B=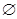 ,求a的取值范围。
,求a的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com