练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

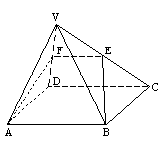
    已知正四棱锥V－ABCD的侧面VAB与底面成60°的二面角，截面ABEF平分此二面角，交平面VCD于EF．求证：平面ABEF⊥平面VCD

     

    答案：
    解析：

    证：设V在底面的射影为O，VO与平面ABEF的交点为M，分别取AB、CD中点G、H，连结VG、VH，连GM延长交EF于N，则∠ VGO=60°,

    　　∵VG=VH，∴△VGH为正三角形，

    　　∵∠MGO=30°，∴GN⊥VH，

    　　∵四边形ABCD为正方形，∴GH⊥AB

    　　∴GN⊥AB

    　　∴EF∥AB

    　　∴GN⊥EF

    　　∴GN⊥平面VCD

    　　

    　　∴平面ABEF⊥平面VCD．

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

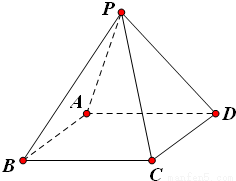
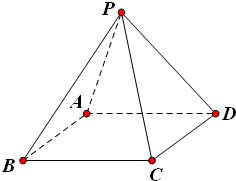    精英家教网已知正四棱锥P-ABCD的全面积为2，记正四棱锥的高为h．
    （1）用h表示底面边长，并求正四棱锥体积V的最大值；
    （2）当V取最大值时，求异面直线AB和PD所成角的大小．
    （结果用反三角函数值表示）

    查看答案和解析>>

    科目：高中数学 来源：学习周报　数学　人教课标高一版(A必修2)　2009－2010学年　第23期　总179期 人教课标高一版 题型：044

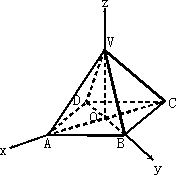
    已知正四棱锥V－ABCD中，O为底面中心，|AB|＝2，|VO|＝3，以O为坐标原点，射线OA为x轴，射线OB为y轴，射线OV为z轴，建立如图所示的空间直角坐标系Oxyz，试确定各顶点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知正四棱锥P-ABCD的全面积为2，记正四棱锥的高为h．
    （1）用h表示底面边长，并求正四棱锥体积V的最大值；
    （2）当V取最大值时，求异面直线AB和PD所成角的大小．
    （结果用反三角函数值表示）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分.

    已知正四棱锥P-ABCD的全面积为2，记正四棱锥的高为h．

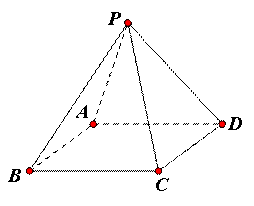    （1）用h表示底面边长,并求正四棱锥体积V的最大值；

    （2）当取最大值时，求异面直线AB和PD所成角的大小.

    （结果用反三角函数值表示）

    查看答案和解析>>

    科目：高中数学 来源：2011年上海市宝山区高考数学一模试卷（文理合卷）（解析版） 题型：解答题

    已知正四棱锥P-ABCD的全面积为2，记正四棱锥的高为h．
    （1）用h表示底面边长，并求正四棱锥体积V的最大值；
    （2）当V取最大值时，求异面直线AB和PD所成角的大小．
    （结果用反三角函数值表示）

    查看答案和解析>>

    同步练习册答案