
分析 (1)令t=$\frac{2{x}^{2}+3}{{x}^{2}+1}$,可得t∈(2,3],且t=$\frac{2{x}^{2}+3}{{x}^{2}+1}$在(-∞,0]上为增函数,在[0,+∞)上为减函数,结合二次函数的图象和性质及复合函数同增异减的原则,可得函数f($\frac{2{x}^{2}+3}{{x}^{2}+1}$)的单调区间;
(2)?x∈R,都有f(x)≥|x|成立,可得当x≤0时,b≤-1,或$\left\{\begin{array}{l}b>-1\\ 4a-{(b+1)}^{2}≥0\end{array}\right.$;当x>0时,b≥1,或$\left\{\begin{array}{l}b<1\\ 4a-{(b-1)}^{2}≥0\end{array}\right.$,进而得到4a-b2的最小值.
解答 解:(1)令t=$\frac{2{x}^{2}+3}{{x}^{2}+1}$=2+$\frac{1}{{x}^{2}+1}$,
则t∈(2,3],且t=$\frac{2{x}^{2}+3}{{x}^{2}+1}$在(-∞,0]上为增函数,在[0,+∞)上为减函数;
由函数f(x)=ax2+bx+1(a>0),可得f(0)=1,
若?x∈R,函数f($\frac{2{x}^{2}+3}{{x}^{2}+1}$)有最大值1,则f(3)=1,
则函数f(x)在(2,3]上为增函数,
故函数f($\frac{2{x}^{2}+3}{{x}^{2}+1}$)的单调递增区间为(-∞,0],单调递减区间为[0,+∞);
(2)当x≤0时,f(x)≥|x|可化为:ax2+(b+1)x+1≥0,则$-\frac{b+1}{2}≥0$,或$\left\{\begin{array}{l}-\frac{b+1}{2}<0\\ \frac{4a-{(b+1)}^{2}}{4a}≥0\end{array}\right.$,即b≤-1,或$\left\{\begin{array}{l}b>-1\\ 4a-{(b+1)}^{2}≥0\end{array}\right.$,
当x>0时,f(x)≥|x|可化为:ax2+(b-1)x+1≥0,则$-\frac{b-1}{2}≤0$,或$\left\{\begin{array}{l}-\frac{b-1}{2}>0\\ \frac{4a-{(b-1)}^{2}}{4a}≥0\end{array}\right.$,即b≥1,或$\left\{\begin{array}{l}b<1\\ 4a-{(b-1)}^{2}≥0\end{array}\right.$,
则b≤-1时,4a-(b-1)2≥0,即4a-b2≥1-2b≥3;
-1<b<1时,4a-(b-1)2≥0且4a-(b+1)2≥0,即4a-b2≥1-2b≥3且4a-b2≥1+2b≥3;
b≥1时,4a-(b+1)2≥0,即4a-b2≥1+2b≥3;
综上可得4a-b2的最小值为3.
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


科目:高中数学 来源: 题型:选择题
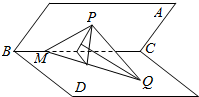 如图所示,二面角A-BC-D的大小为45°,P为平面ABC内一点,Q为平面BCD内一点,M为BC上一点,已知P在平面BCD内的射影恰好在线段MQ上,设PM=$\sqrt{2}$,∠CMQ=45°,直线PQ与平面BCD所成的角为30°,则PQ的长为( )
如图所示,二面角A-BC-D的大小为45°,P为平面ABC内一点,Q为平面BCD内一点,M为BC上一点,已知P在平面BCD内的射影恰好在线段MQ上,设PM=$\sqrt{2}$,∠CMQ=45°,直线PQ与平面BCD所成的角为30°,则PQ的长为( )| A. | $\frac{2}{3}\sqrt{6}$ | B. | $\frac{3}{4}\sqrt{6}$ | C. | $\frac{4}{3}\sqrt{2}$ | D. | $\frac{3}{2}\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | $\sqrt{41}$ | C. | $\sqrt{41}$-2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,ABCD是边长为2的正方形,ED=1,DE⊥平面ABCD,EF∥BD,且EF=$\frac{1}{2}$BD.
如图,ABCD是边长为2的正方形,ED=1,DE⊥平面ABCD,EF∥BD,且EF=$\frac{1}{2}$BD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com