
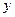 (百件)与销售单价
(百件)与销售单价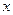 (元/件)之间的关系用下图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.
(元/件)之间的关系用下图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.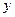 表示为
表示为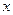 的函数;
的函数;
科目:高中数学 来源:不详 题型:解答题
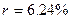 ,2000年该奖发放后基金总额约为21000万元。用
,2000年该奖发放后基金总额约为21000万元。用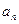
 表示为第
表示为第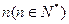 年该奖发放后的基金总额(2000年为第一年)。
年该奖发放后的基金总额(2000年为第一年)。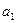 表示
表示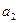 与
与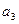 ,并根据所求结果归纳出
,并根据所求结果归纳出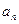 的表达式;
的表达式;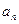 的表达式判断2011年度该奖各项奖金是否超过150万元?并计算从2001年到2011年该奖金累计发放的总额。
的表达式判断2011年度该奖各项奖金是否超过150万元?并计算从2001年到2011年该奖金累计发放的总额。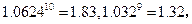
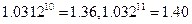 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
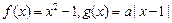 .
.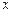 的方程
的方程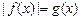 只有一个实数解,求实数
只有一个实数解,求实数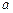 的取值范围;
的取值范围;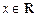 时,不等式
时,不等式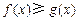 恒成立,求实数
恒成立,求实数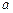 的取值范围;
的取值范围;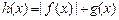 在区间
在区间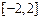 上的最大值(直接写出结果,不需给出演算步骤).
上的最大值(直接写出结果,不需给出演算步骤).查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 在定义域内是增函数;③函数
在定义域内是增函数;③函数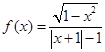 图象关于原点对称;④既是奇函数又是偶函数的函数一定是
图象关于原点对称;④既是奇函数又是偶函数的函数一定是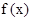 ="0"
="0" 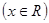 ; ⑤函数y=f(x+2)图象与函数y=f(2-x)图象关于直线x=2对称;其中正确命题的个数为:( )
; ⑤函数y=f(x+2)图象与函数y=f(2-x)图象关于直线x=2对称;其中正确命题的个数为:( )| A.0个 | B.1个 | C.2个 | D.3个 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
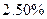 保持不变,到2015年9月1日将所有的存款和利息全部取出,他可取回的钱数约为
保持不变,到2015年9月1日将所有的存款和利息全部取出,他可取回的钱数约为  【 】
【 】| A.11314元 | B.53877元 | C.11597元 | D.63877元 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
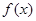 的值域是其定义域的子集,那么
的值域是其定义域的子集,那么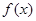 叫做“集中函数”,则下列函数:
叫做“集中函数”,则下列函数: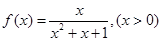 , ②
, ②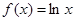
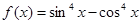
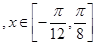 , ④
, ④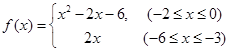
 (请把符合
(请把符合 条件的序号全部填在横线上)
条件的序号全部填在横线上)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com