
函数f(x)="sin" (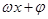 )的导函数
)的导函数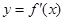 的部分图像如图所示,其中,P为图像与y轴的交点,A,C为图像与x轴的两个交点,B为图像的最低点.
的部分图像如图所示,其中,P为图像与y轴的交点,A,C为图像与x轴的两个交点,B为图像的最低点.

(1)若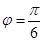 ,点P的坐标为(0,
,点P的坐标为(0,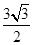 ),则
),则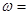 ;
;
(2)若在曲线段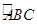 与x轴所围成的区域内随机取一点,则该点在△ABC内的概率为 .
与x轴所围成的区域内随机取一点,则该点在△ABC内的概率为 .
3,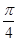
【解析】
试题分析:(1)先利用导数的运算性质,求函数f(x)的导函数f′(x),再将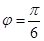 ,f′(0)=
,f′(0)=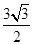 代入导函数解析式,即可解得ω的值;(2)先利用定积分的几何意义,求曲线段
代入导函数解析式,即可解得ω的值;(2)先利用定积分的几何意义,求曲线段 与x轴所围成的区域面积,再求三角形ABC的面积,最后利用几何概型概率计算公式求面积之比即可得所求概率。解:(1)∵函数f(x)="sin" (ωx+φ)的导函数y=f′(x)=ωcos(ωx+φ),其中
与x轴所围成的区域面积,再求三角形ABC的面积,最后利用几何概型概率计算公式求面积之比即可得所求概率。解:(1)∵函数f(x)="sin" (ωx+φ)的导函数y=f′(x)=ωcos(ωx+φ),其中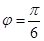 ,过点P(0,
,过点P(0,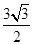 ),∴ωcos
),∴ωcos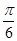 =
=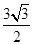 ∴ω=3,故答案为 3,
∴ω=3,故答案为 3,
(2)∵f′(x)=ωcos(ωx+φ),∴曲线段 与x轴所围成的区域面积为
与x轴所围成的区域面积为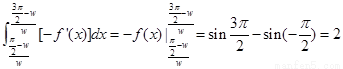 ,三角形ABC的面积为
,三角形ABC的面积为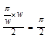 ,∴在曲线段
,∴在曲线段 与x轴所围成的区域内随机取一点,则该点在△ABC内的概率为
与x轴所围成的区域内随机取一点,则该点在△ABC内的概率为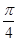 ,故答案为3,
,故答案为3,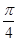
考点:f(x)=Asin (ωx+φ)型函数的图象
点评:本题主要考查了f(x)=Asin (ωx+φ)型函数的图象和性质,导数运算及导函数与原函数的关系,定积分的几何意义,几何概型概率的计算方法,属基础题


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2015届广东揭阳一中高一下学期第二次阶段考试文科数学试卷(解析版) 题型:选择题
若动直线x=a与函数f(x)="sin" x和g(x)="cos" x的图像分别交于M、N两点,则|MN|的最大值为 ( )
A.1 B.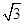 C.
C.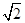 D.2
D.2
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省绍兴市高一下学期期中考试文科数学试卷(解析版) 题型:选择题
定义在(-∞,0)∪(0,+∞)上的函数f(x),如果对于任意给定的等比数列{an},{f(an)}仍是等比数列,则称f(x)为“保等比数列函数”。现有定义在( )
(-∞,0)∪(0,+∞)上的如下函数:①f(x)=x²;②f(x)=2x;③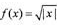 ;④f(x)="ln|x" |。则其中是“保等比数列函数”的f(x)的序号为 ( )
;④f(x)="ln|x" |。则其中是“保等比数列函数”的f(x)的序号为 ( )
A.①② B.①③ C.③④ D.②④
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省深圳市高三第一次调研考试理科数学试卷(解析版) 题型:解答题
已知函数f(x)="2" sin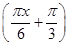 (0≤x≤5),点A、B分别是函数y=f(x)图像上的最高点和最低点.
(0≤x≤5),点A、B分别是函数y=f(x)图像上的最高点和最低点.
(1)求点A、B的坐标以及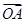 ·
· 的值;
的值;
(2)没点A、B分别在角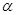 、
、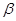 的终边上,求tan(
的终边上,求tan(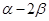 )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省武汉市武昌区高三上学期期末调研测试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知函数f(x)=" cos(" 2x+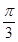 )+sin2x.
)+sin2x.
(Ⅰ)求函数f(x)的最小正周期和值域;
(Ⅱ)在△ABC中,角A、B、C的对边分别为a、b、c,满足
2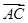 ·
·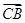 =
=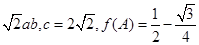 , 求△ABC的面积S.
, 求△ABC的面积S.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com