
分析 (1)设与直线l:3x-4y+4=0垂直的直线方程为4x+3y+c=0,把点(-2,2)代入,能求出结果.
(2)设与直线l平行且距离为2的直线方程为3x-4y+c=0,由平行线间的距离公式能求出结果.
解答 解:(1)设与直线l:3x-4y+4=0垂直的直线方程为4x+3y+c=0,
把点(-2,2)代入,得:-8+6+c=0,解得c=2,
∴过点(-2,2)且与直线l垂直的直线方程为:4x+3y+2=0.
(2)设与直线l平行且距离为2的直线方程为3x-4y+c=0,
则$\frac{|c-4|}{\sqrt{9+16}}$=2,
解得c=14或c=2.
∴与直线l平行且距离为2的直线方程为3x-4y+2=0或3x-4y+14=0.
点评 本题考查直线方程的求法,是基础题,解题时要认真审题,注意直线与直线平行、直线与直线垂直的性质的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1+a8=a4+a5 | B. | a1+a8<a4+a5 | ||
| C. | a1+a8>a4+a5 | D. | a1+a8与a4+a5大小关系不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
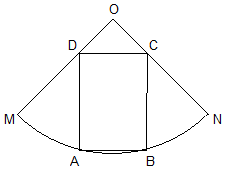 如图,有一块扇形草地OMN,已知半径为R,∠MON=$\frac{π}{2}$,现要在其中圈出一块矩形场地ABCD作为儿童乐园使用,其中点A、B在弧MN上,且线段AB平行于线段MN
如图,有一块扇形草地OMN,已知半径为R,∠MON=$\frac{π}{2}$,现要在其中圈出一块矩形场地ABCD作为儿童乐园使用,其中点A、B在弧MN上,且线段AB平行于线段MN查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{20}$=1 | B. | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{5}$=1 | C. | $\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{20}$=1 | D. | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{25}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 患呼吸系统疾病 | 未患呼吸系统疾病 | 总计 | |
| 重污染地区 | 103 | 1 397 | 1 500 |
| 轻污染地区 | 13 | 1 487 | 1 500 |
| 总计 | 116 | 2 884 | 3 000 |
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com