分析:( i )根据题意可得函数的定义域为(0,+∞),然后对函数求导可得f′(x)=2a+
+
.∵f(x)在x=1,x=-
处取得极值,∴f′(1)=0,f′(
)=0,可求,b的值;
(ii)在[
,2]存在存在x
0,使得不等式f(x
0)-c≤0,只需c≥[f(x)]
min,可解.
解答:解:(i)∵f(x)=2ax-
+lnx,定义域为(0,+∞),
∴f′(x)=2a+
+
.
∵f(x)在x=1,x=-
处取得极值,
∴f′(1)=0,f′(
)=0,
即
,
解得:
,
∴所求a,b的值为-
,-
;
(ii)在[
,2]存在存在x
0,使得不等式f(x
0)-c≤0,只需c≥[f(x)]
min,
由f′(x)=-
x-
+
=-
=-
,
∴当x∈[
,
]时,f′(x)<0,故f(x)在[
,
]是单调递减,
当x∈[
,1]时,f′(x)>0,故f(x)在[
,1]是单调递增,
当x∈[1,2]时,f′(x)<0,故f(x)在[1,2]是单调递减;
∴f(
)是f(x)在[
,2]上的极小值,
而f(
)=
+ln
=
-ln2,f(2)=-
+ln2,
且f(
)-f(2)=
-ln4=ln
e-ln4,
又e
3-16>0,
∴ln
e-ln4>0,
∴[f(x)]
min=f(2),
∴c≥[f(x)]
min=-
+ln2,
∴c的取值范围为[-
+ln2,+∞),
∴c的最小值为
+ln2.
点评:(1)若函数在某点取得极值则该店的导数为0是导数最基本的考查
(2)函数的存在性问题、恒成立问题常转化为求解函数的最值问题,结合导数的知识可求



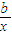 +lnx,若f(x)在x=1,x=-
+lnx,若f(x)在x=1,x=- 处取得极值,
处取得极值, ,2]存在x,使得不等式f(x)-c≤0,求c的最小值.
,2]存在x,使得不等式f(x)-c≤0,求c的最小值.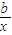 +lnx,若f(x)在x=1,x=-
+lnx,若f(x)在x=1,x=- 处取得极值,
处取得极值, ,2]存在x,使得不等式f(x)-c≤0,求c的最小值.
,2]存在x,使得不等式f(x)-c≤0,求c的最小值.