
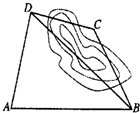
 如图,为了计算郑东新区龙湖岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两个测量点,现测得AD⊥CD,AD=5km,AB=7km,∠BDA=60°,∠BCD=135°,求两景点B与C的距离.(假设A,B,C,D在同一平面内)
如图,为了计算郑东新区龙湖岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两个测量点,现测得AD⊥CD,AD=5km,AB=7km,∠BDA=60°,∠BCD=135°,求两景点B与C的距离.(假设A,B,C,D在同一平面内)| BDsin∠CDB |
| sin∠BCD |
| 2 |
| BC |
| sin∠CDB |
| BD |
| sin∠BCD |
| BDsin∠CDB |
| sin∠BCD |
| 8sin30° |
| sin135° |
| 2 |
| 2 |


科目:高中数学 来源: 题型:
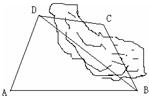 如图,为了计算某湖岸边两景点B与C的距离,由于地形的限制,需要在岸上A和D两个测量点,现测得AD⊥CD,AD=10km,AB=14km,∠BDA=60°,∠BCD=135°,求两景点B与C之间的距离(假设A、B、C、D在同一平面内,测量结果精确到0.1km,参考数据:
如图,为了计算某湖岸边两景点B与C的距离,由于地形的限制,需要在岸上A和D两个测量点,现测得AD⊥CD,AD=10km,AB=14km,∠BDA=60°,∠BCD=135°,求两景点B与C之间的距离(假设A、B、C、D在同一平面内,测量结果精确到0.1km,参考数据:| 2 |
| 3 |
| 5 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东北江中学第一学期期末考试高二理科数学 题型:解答题
如图,为了计算北江岸边两景点 与
与 的距离,由于地形的限制,需要在岸上选取
的距离,由于地形的限制,需要在岸上选取 和
和 两个测量点,现测得
两个测量点,现测得 ,
, ,
, ,
, ,
, ,求两景点
,求两景点 与
与 的距离(假设
的距离(假设 在同一平面内,测量结果保留整数;参考数据:
在同一平面内,测量结果保留整数;参考数据: )
)
查看答案和解析>>
科目:高中数学 来源:2010年陕西省高三第七次适应性考试数学(理) 题型:解答题
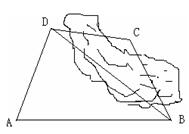
如图,为了计算某湖岸边两景点B与C的距离,由于地形的限制,需要在岸上A和D两个测量点,现测得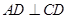 ,AD=10km,AB=14km,
,AD=10km,AB=14km, 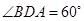 ,
,  ,求两景点B与C之间的距离(假设A、B、C、D在同一平面内,测量结果精确到0.1km,参考数据:
,求两景点B与C之间的距离(假设A、B、C、D在同一平面内,测量结果精确到0.1km,参考数据: )
)
查看答案和解析>>
科目:高中数学 来源:2012届广东北江中学第一学期期末考试高二理科数学 题型:解答题
如图,为了计算北江岸边两景点 与
与 的距离,由于地形的限制,需要在岸上选取
的距离,由于地形的限制,需要在岸上选取 和
和 两个测量点,现测得
两个测量点,现测得 ,
, ,
, ,
, ,
, ,求两景点
,求两景点 与
与 的距离(假设
的距离(假设 在同一平面内,测量结果保留整数;参考数据:
在同一平面内,测量结果保留整数;参考数据: )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com