函数f(x)的定义域为D={x|x≠0},且满足对于任意x1,x2∈D,有f(x1•x2)=f(x1)+f(x2).
(1)求f(1)和f(-1)的值;
(2)判断f(x)的奇偶性并证明;
(3)若f(4)=1,f(3x+4)<2,且f(x)在(0,+∞)上是增函数,求x的取值范围.
解:(1)令x
1=x
2=1,有f(1)=f(1)+f(1),
所以f(1)=0.
令x
1=x
2=-1,有f(1)=f(-1)+f(-1)=0,
所以f(-1)=0.
(2)f(x)为偶函数,证明如下:
令x
1=-1,有f(-x
2)=f(-1)+f(x
2),
∴f(-x
2)=f(x
2),
又定义域关于原点对称,所以f(x)为偶函数.
(3)因为f(4)=1,所以f(16)=f(4)+f(4)=2,
所以f(3x+4)<f(16),
又函数为偶函数,所以f(|3x+4|)<f(16),
所以
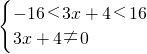
,解得x的取值范围是:-

<x<4且x≠-

.
分析:(1)赋值法:令x
1=x
2=1,可求f(1),令x
1=x
2=-1,可求f(-1);
(2)令x
1=-1,根据函数奇偶性的定义即可判断;
(3)由f(4)=1,得f(16)=f(4)+f(4)=2,从而不等式可化为f(3x+4)<f(16),借助函数的奇偶性、单调性可去掉不等式中的符号“f”,解不等式组即可.
点评:本题考查抽象函数的奇偶性、单调性及抽象不等式的求解,定义、性质是解决抽象函数问题的基本方法.

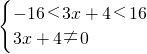 ,解得x的取值范围是:-
,解得x的取值范围是:- <x<4且x≠-
<x<4且x≠- .
.
