
如图,在正方体 中,
中,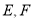 分别是
分别是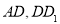 中点.
中点.

求证:(1)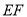 ∥平面
∥平面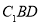 ;
;
(2)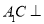 平面
平面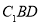 .
.
(1)详见解析(2)详见解析
【解析】
试题分析:
(1)利用正方体的性质和三角形中位线性质可得EF∥AD1,进而利用平行四边形ABC1D1转化为EF∥BC1,最后利用线面平行的判定定理证得结论.
(2)首先利用侧棱垂直于底面得到AA1⊥BD,然后结合正方形性质有AC⊥BD即可证得BD⊥平面AA1C,同理可证A1C⊥BC1最后利用线面垂直的判定定理即得结论.
试题解析:

证明:(1)连结A1D,
∵ E,F分别是AD和DD1的中点,∴ EF∥AD1 . 2分
∵ 正方体ABCD-A1B1C1D1,
∴ AB∥D1C1,AB=D1C1.
∴ 四边形ABC1D1为平行四边形,即有A1D∥BC1 4分
∴ EF∥BC1.
又EF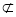 平面C1BD,BC1
平面C1BD,BC1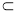 平面C1BD,
平面C1BD,
∴ EF∥平面AB1D1. 7分
(2)连结AC,则AC⊥BD.
∵ 正方体ABCD-A1B1C1D1,∴AA1⊥平面ABCD,
∴ AA1⊥BD.
又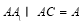 ,∴BD⊥平面AA1C,
,∴BD⊥平面AA1C,
∴ A1C⊥BD. 11分
同理可证A1C⊥BC1.
又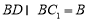 ,∴A1C⊥平面C1BD. 14分
,∴A1C⊥平面C1BD. 14分
考点:线面平行的判定定理,线面垂直的判定定理
考点分析: 考点1:点、线、面之间的位置关系 试题属性

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年江苏省扬州市高三上学期期末理科数学试卷(解析版) 题型:解答题
已知函数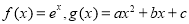 。
。
(1)若f(x)的图象与g(x)的图象所在两条曲线的一个公共点在y轴上,且在该点处两条曲线的切线互相垂直,求b和c的值。
(2)若a=c=1,b=0,试比较f(x)与g(x)的大小,并说明理由;
(3)若b=c=0,证明:对任意给定的正数a,总存在正数m,使得当x 时,
时,
恒有f(x)>g(x)成立。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省泰州市高三上学期期末考试理科数学试卷(解析版) 题型:解答题
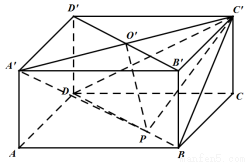
(本小题满分10分)如图,在长方体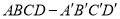 中,
中,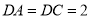 ,
,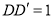 ,
,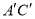 与
与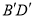 相交于点
相交于点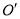 ,点
,点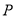 在线段
在线段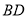 上(点
上(点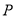 与点
与点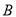 不重合).
不重合).
(1)若异面直线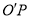 与
与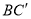 所成角的余弦值为
所成角的余弦值为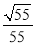 ,求
,求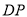 的长度;
的长度;
(2)若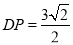 ,求平面
,求平面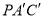 与平面
与平面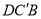 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省苏州市高三上学期期末考试文科数学试卷(解析版) 题型:填空题
某课题组进行城市空气质量监测,按地域将24个城市分成甲、乙、丙三组,对应区域城市数分别为4、12、8.若用分层抽样抽取6个城市,则乙组中应该抽取的城市数为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省常州市高三上学期期末调研测试文科数学试卷(解析版) 题型:填空题
现有5道试题,其中甲类试题2道,乙类试题3道,现从中随机取2道试题,则至少有1道试题是乙类试题的概率为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年贵州省贵阳市高三上学期期末监测考试文科数学试卷(解析版) 题型:填空题
某学生在复习函数内容时,得出如下一些结论:
①函数 在
在 上有最大值
上有最大值 ;
;
②函数 在
在 上是减函数;
上是减函数;
③ ,使函数
,使函数 为奇函数;
为奇函数;
④对数函数具有性质“对任意实数 ,
, ,满足
,满足 ”
”
其中正确的结论是_______.(填写你认为正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com