
| 1 |
| 7 |
. |
| B |
| 1 |
| 7 |
| 1 |
| 7 |
. |
| B |
. |
| B |
| ||
|
| 6 |
| 7 |
| 6 |
| 7 |
| 12 | ||
|
| 2 |
| 7 |
| 10 | ||
|
| 5 |
| 21 |
| 8 | ||
|
| 4 |
| 21 |
| 6 | ||
|
| 1 |
| 7 |
| 4 | ||
|
| 2 |
| 21 |
| 2 | ||
|
| 1 |
| 21 |
| X | 0 | 1 | 2 | 3 | 4 | 5 | ||||||||||||
| P |
|
|
|
|
|
|
| 2 |
| 7 |
| 5 |
| 21 |
| 4 |
| 21 |
| 1 |
| 7 |
| 2 |
| 21 |
| 1 |
| 21 |
| 5 |
| 3 |


科目:高中数学 来源:2011-2012学年福建省高三第八次月考理科数学试卷 题型:解答题
有甲、乙等7名选手参加一次演讲比赛,采用抽签的方式随机确定每名选手的演出顺序(序号为1,2,…,7).
(Ⅰ)甲选手的演出序号是1的概率;
(Ⅱ)求甲、乙两名选手的演出序号至少有一个为奇数的概率;
(Ⅲ)设在甲、乙两名选手之间的演讲选手个数为 ,求
,求 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:
有甲、乙等7名选手参加一次讲演比赛,采用抽签的方式随机确定每名选手的演出顺序(序号为1,2,…,7)。
(1)甲选手的演出序号是1的概率;
(2)求甲、乙两名选手的演出序号至少有一个为奇数的概率;
(3)求甲、乙两名选手之间的演讲选手个数![]() 的分布列与期望。
的分布列与期望。
查看答案和解析>>
科目:高中数学 来源:福建省龙岩一中2011-2012学年高三下学期第八次月考试卷数学(理) 题型:解答题
有甲、乙等7名选手参加一次演讲比赛,采用抽签的方式随机确定每名选手的演出顺序(序
号为1,2,…,7).
(Ⅰ)甲选手的演出序号是1的概率;
(Ⅱ)求甲、乙两名选手的演出序号至少有一个为奇数的概率;
(Ⅲ)设在甲、乙两名选手之间的演讲选手个数为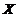 ,求
,求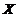 的分布列与期望.
的分布列与期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com