
分析 (I)利用等差数列的通项公式即可得出;
(II)利用等差数列的前n项和公式即可得出;
(III)利用等比数列的前n项和公式即可得出.
解答 解:(Ⅰ)设等差数列{an}的公差为d,
∵a1+a4+a7=9,a3+a6+a9=21,
得$\left\{{\begin{array}{l}{3{a_1}+9d=9}\\{3{a_1}+15d=21}\end{array}}\right.⇒\left\{{\begin{array}{l}{{a_1}+3d=3}\\{{a_1}+5d=7}\end{array}}\right.$,
解得a1=-3,d=2,
∴an=2n-5.
(Ⅱ)S9=9a1+36d=9×(-3)+36×2=45.
(Ⅲ)由(Ⅰ)${c_n}={2^{{a_n}+3}}={2^{2(n-1)}}={4^{n-1}}$,
∴{cn}是首项c1=1,公比q=4的等比数列,
∴$T{\;}_n=\frac{{{c_1}(1-{q^n})}}{1-q}=\frac{{{4^n}-1}}{3}$.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
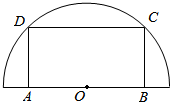 如图,在半径为30cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.
如图,在半径为30cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $({-\frac{11}{3},\frac{13}{3}})$ | B. | $({\frac{1}{3},\;\frac{7}{3}})$ | C. | $({-\frac{5}{3},\frac{55}{3}})$ | D. | $({-\frac{5}{3},\;\frac{7}{3}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 关于直线y=x对称 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com