
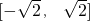
 sin(x+
sin(x+ ),根据-1≤sin(x-
),根据-1≤sin(x- )≤1,得到-
)≤1,得到- ≤
≤ sin(x-
sin(x- )≤
)≤ ,从而得到函数y的值域.
,从而得到函数y的值域. sin(x-
sin(x- ),
), )≤1,∴-
)≤1,∴- ≤
≤ sin(x-
sin(x- )≤
)≤ ,
,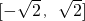 ,
, sin(x+
sin(x+ ),
), )≤1,∴-
)≤1,∴- ≤
≤ sin(x+
sin(x+ )≤
)≤ ,
,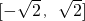 ,
,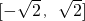 ,
,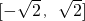


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
 如图,已知函数y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),若随机向圆O:x2+y2=π2内投入一米粒,则该米粒落在区域M内的概率是( )
如图,已知函数y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),若随机向圆O:x2+y2=π2内投入一米粒,则该米粒落在区域M内的概率是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com