
函数 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A. | B. | C. | D. |
B
解析试题分析:因为求解函数 的零点所在的区间,只要保证端点值的函数值异号即可,那么由于f(2)=ln2-1<0,f(e)=lne-
的零点所在的区间,只要保证端点值的函数值异号即可,那么由于f(2)=ln2-1<0,f(e)=lne-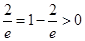 ,且在定义域内连续的函数,则可知选B。而选项A,C,D的端点值函数值同号,舍去。也可以通过函数的单调性可知,函数是定义域上增函数,由于f(2)<0,f(e)>0,可知f(1)<0, f(3)>0,故选B.
,且在定义域内连续的函数,则可知选B。而选项A,C,D的端点值函数值同号,舍去。也可以通过函数的单调性可知,函数是定义域上增函数,由于f(2)<0,f(e)>0,可知f(1)<0, f(3)>0,故选B.
考点:本试题主要是考查了函数的零点的概念,以及基本初等函数的零点所在的区间问题,可以根据判定定理,也可以结合图象与图像来进行,考查了分析问题和解决问题的能力。
点评:确定零点所在的区间,利用零点存在性定理可以逐一分析证明,也可以利用图像与图像的交点问题来分析。同时能注意到函数的单调性,将给判定符号带来方便之处。


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:单选题
函数 其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:
其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:
①若P∩M= ,则f(P)∩f(M)=
,则f(P)∩f(M)= ;
;
②若P∩M≠ ,则f(P)∩f(M) ≠
,则f(P)∩f(M) ≠ ;
;
③若P∪M=R,则f(P)∪f(M)=R;
④若P∪M≠R,则f(P)∪f(M)≠R.
其中正确判断有( )
A 0个 B 1个 C 2个 D 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com