Question

10．已知x∈R，符号[x]表示不超过x的最大整数，如[1.9]=1，[2.01]=2．若函数$f（x）=\frac{x}{[x]}-m$（x≥1）有且仅有三个零点，则m的取值范围是（　　）

• A． $[{\frac{3}{2}，2}]$
• B． $[{\frac{3}{2}，2}）$
• C． $[{\frac{5}{4}，\frac{4}{3}}）$
• D． $[{\frac{5}{4}，\frac{4}{3}}]$

Answer 1

分析 由f（x）=0得 $\frac{x}{[x]}$=m，令g（x）=$\frac{x}{[x]}$，作出g（x）的图象，利用数形结合即可得到a的取值范围．

解答 解：由f（x）=$\frac{x}{[x]}$-m=0得：$\frac{x}{[x]}$=m，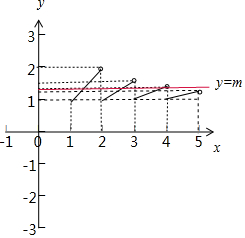
当1≤x＜2，[x]=1，此时g（x）=x，此时1≤g（x）＜2，
当2≤x＜3，[x]=2，此时g（x）=$\frac{1}{2}x$，此时1≤g（x）＜$\frac{3}{2}$，
当3≤x＜4，[x]=3，此时g（x）=$\frac{1}{3}x$，此时≤1g（x）＜$\frac{4}{3}$，
当4≤x＜5，[x]=4，此时g（x）=$\frac{1}{4}$x，此时1≤g（x）＜$\frac{5}{4}$，
作出函数g（x）的图象，
要使函数$f（x）=\frac{x}{[x]}-m$（x≥1）有且仅有三个零点，
即函数g（x）=m有且仅有三个零点，
则由图象可知$\frac{5}{4}$≤m$＜\frac{4}{3}$，
故选：C．

点评 本题主要考查函数零点的应用，根据函数和方程之间的关系构造函数g（x），利用数形结合是解决本题的关键．难度较大．