
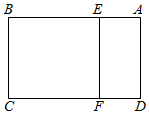
 如图,在矩形ABCD中,AD=$\sqrt{5}$,AB=3,E、F分别为AB边、CD边上一点,且AE=DF=l,现将矩形ABCD沿EF折起,使得平面ADFE⊥平面BCFE,连接AB、CD,则所得三棱柱ABE-DCF的侧面积比原矩形ABCD的面积大约多(取$\sqrt{5}$≈2.236)( )
如图,在矩形ABCD中,AD=$\sqrt{5}$,AB=3,E、F分别为AB边、CD边上一点,且AE=DF=l,现将矩形ABCD沿EF折起,使得平面ADFE⊥平面BCFE,连接AB、CD,则所得三棱柱ABE-DCF的侧面积比原矩形ABCD的面积大约多(取$\sqrt{5}$≈2.236)( )| A. | 68% | B. | 70% | C. | 72% | D. | 75% |
分析 根据题意求出三棱柱ABE-DCF的侧面积增加的部分与原来矩形ABCD的面积之比可得答案.
解答 解:将矩形ABCD沿EF折起,使得平面ADFE⊥平面BCFE,可得三棱柱ABE-DCF,(如图)
侧面积增加的部分为ABCD,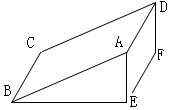
∵EB⊥BC,△ABE是直角三角形,
∴AB⊥BC.
同理可证ABCD是矩形.
∵AE=DF=1.AB=3,AD=$\sqrt{5}$,
∴BE=2
∴AB=$\sqrt{5}$
故得侧面积增加的部分为$S=\sqrt{5}×\sqrt{5}=5$.
侧面积比原矩形ABCD的面积大约多出$\frac{5}{3\sqrt{5}}=\frac{\sqrt{5}}{3}=\frac{2.236}{3}=75$%
故选D.
点评 本题考查了三棱柱的侧面积和图形对折后的画法,考查学生对书本知识的掌握情况以及空间想象、推理能力,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x<4} | B. | {x|x≤3或x≥4} | C. | {x|-1≤x≤1且x≠0} | D. | {x|-1≤x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2n-3 | B. | 2n-4 | C. | n-3 | D. | n-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{3}$ | B. | 16 | C. | 8 | D. | $\frac{{16\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com