
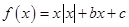 ,给出下列4个命题:
,给出下列4个命题: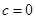 时,
时,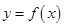 是奇函数;2,
是奇函数;2,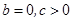 时,方程
时,方程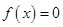 只有一个实根;
只有一个实根;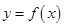 的图像关于点
的图像关于点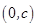 对称;4,方程
对称;4,方程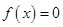 至多有两个实根.
至多有两个实根.科目:高中数学 来源:不详 题型:填空题
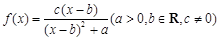 ,函数
,函数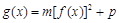 (
(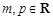 ,且mp<0),给出下列结论:
,且mp<0),给出下列结论: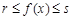 对于任意实数x恒成立;
对于任意实数x恒成立; 的图像关于点
的图像关于点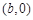 对称;
对称; 可能不存在零点(注:使关于x的方程
可能不存在零点(注:使关于x的方程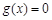 的实数x叫做函数
的实数x叫做函数 的零点);
的零点);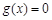 的解集可能为{-1,1,4,5}.
的解集可能为{-1,1,4,5}.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
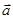 ,
, 的夹角为锐角”的充要条件是“
的夹角为锐角”的充要条件是“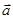 ·
· >0”;
>0”; )>
)>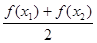 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
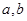 ,如果
,如果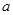 平行于平面
平行于平面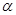 ,那么
,那么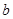 不平行平面
不平行平面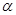 ;
;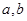 ,如果
,如果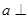 平面
平面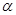 ,那么
,那么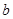 不垂直于平面
不垂直于平面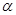 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
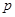 且
且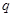 是真命题”, 命题乙:“
是真命题”, 命题乙:“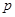 或
或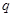 是真命题”,则命题甲是命题乙的
是真命题”,则命题甲是命题乙的 | A.充要条件 | B.必要不充分条件 |
| C.充分不必要条件 | D.既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,则
,则 不全为零”的否命题; ②“等腰三角形都相似”的逆命题; ③“若
不全为零”的否命题; ②“等腰三角形都相似”的逆命题; ③“若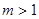 ,则不等式
,则不等式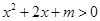 的解集为R”的逆否命题。
的解集为R”的逆否命题。| A.① | B.①③ | C.②③ | D.①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com