
 ,有下列结论:
,有下列结论: ,是一个对数型函数,其内层函数是一个偶函数,故研究这个函数的性质,故只研究x>0时的情况.观察四个选项发现①是关于奇偶性的,②③④与单调性有关,故探究方向出现.
,是一个对数型函数,其内层函数是一个偶函数,故研究这个函数的性质,故只研究x>0时的情况.观察四个选项发现①是关于奇偶性的,②③④与单调性有关,故探究方向出现.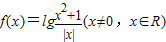 ,是一个对数型函数,其内层函数是一个偶函数,故函数
,是一个对数型函数,其内层函数是一个偶函数,故函数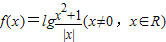 ,是偶函数,其图象关于y轴对称,令x>0,则f(x)=lg
,是偶函数,其图象关于y轴对称,令x>0,则f(x)=lg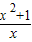 =lg(x+
=lg(x+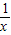 )≥lg2且在(0,1)上是减函数,在(1,+∞)上是增函数.下研究四个选项的正确性;'
)≥lg2且在(0,1)上是减函数,在(1,+∞)上是增函数.下研究四个选项的正确性;'

科目:高中数学 来源:2012-2013学年山东省高三第二次(3月)周测理科数学试卷(解析版) 题型:填空题
关于函数 ,有下列结论:①函数
,有下列结论:①函数 的定义域是(0,+∞);②函数
的定义域是(0,+∞);②函数 是奇函数;③函数
是奇函数;③函数 的最小值为-
的最小值为- ;④当
;④当 时,函数
时,函数 是增函数;当
是增函数;当 时,函数
时,函数 是减函数.
是减函数.
其中正确结论的序号是 .(写出所有你认为正确的结论的序号)
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省淮安市涟水县金城外国语学校高一(下)期初数学试卷(解析版) 题型:填空题
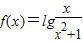 ,有下列结论:
,有下列结论:查看答案和解析>>
科目:高中数学 来源:2010年江苏省南通市海安高级中学高三5月自检数学试卷(1)(解析版) 题型:解答题
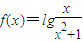 ,有下列结论:
,有下列结论:查看答案和解析>>
科目:高中数学 来源:2011年云南省高三数学一轮复习单元测试02:函数(解析版) 题型:解答题
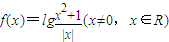 ,有下列结论:
,有下列结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com