
【题目】甲、乙两人各进行3次射击,甲每次击中目标的概率为![]() ,乙每次击中目标的概率为
,乙每次击中目标的概率为![]() 求:(1)甲恰好击中目标2次的概率;(2)乙至少击中目标2次的概率;
求:(1)甲恰好击中目标2次的概率;(2)乙至少击中目标2次的概率;
(3)乙恰好比甲多击中目标2次的概率
【答案】(1)![]() (2);(3)
(2);(3)![]()
【解析】试题分析:(1)由题意知甲射击三次,每次击中目标的概率是定值,可以看作是独立重复试验,根据独立重复试验的公式得到结果;(2)乙射击三次,每次击中目标的概率是定值,可以看作是独立重复试验,乙至少击中目标两次包含击中两次和击中三次,且这两种情况是互斥的,根据公式得到结果;(3)乙恰好比甲多击中目标![]() 次,包含乙恰击中目标
次,包含乙恰击中目标![]() 次且甲恰击中目标零次或乙恰击中目标三次且甲恰击中目标一次,由题意,
次且甲恰击中目标零次或乙恰击中目标三次且甲恰击中目标一次,由题意,![]() 为互斥事件.根据互斥事件和独立重复试验公式得到结果.
为互斥事件.根据互斥事件和独立重复试验公式得到结果.
试题解析:(1)甲恰好击中目标2次的概率为![]()
(2)乙至少击中目标2次的概率为![]()
(3)设乙恰好比甲多击中目标2次为事件A,乙恰好击中目标2次且甲恰好击中目标0次为事件B1,乙恰好击中目标3次且甲恰好击中目标1次为事件B2,则A=B1+B2,B1,B2为互斥事件
P(A)=P(B1)+P(B2)![]()
![]()
所以,乙恰好比甲多击中目标2次的概率为![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在某次水下科研考察活动中,需要潜水员潜入水深为60米的水底进行作业,根据已往经验,潜水员下潜的平均速度为![]() (米/单位时间),每单位时间的用氧量为
(米/单位时间),每单位时间的用氧量为![]() (升),在水底作业10个单位时间,每单位时间用氧量为
(升),在水底作业10个单位时间,每单位时间用氧量为![]() (升),返回水面的平均速度为
(升),返回水面的平均速度为![]() (米/单位时间),每单位时间用氧量为
(米/单位时间),每单位时间用氧量为![]() (升),记该潜水员在此次考察活动中的总用氧量为
(升),记该潜水员在此次考察活动中的总用氧量为![]() (升).
(升).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若![]() ,求当下潜速度
,求当下潜速度![]() 取什么值时,总用氧量最少.
取什么值时,总用氧量最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知右焦点为![]() 的椭圆
的椭圆![]() 过点
过点![]() ,且椭圆
,且椭圆![]() 关于直线
关于直线![]() 对称的图形过坐标原点.
对称的图形过坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且不垂直于
且不垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明:直线
,证明:直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验,为了比较教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如下图:记成绩不低于70分者为“成绩优良”.
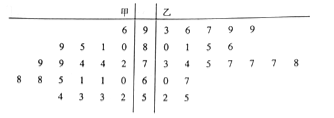
(1)分别计算甲、乙两班20个样本中,化学分数前十的平均分,并大致判断哪种教学方式的教学效果更佳;
(2)由以上统计数据填写下面![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为“成绩优良与教学方式有关”?
的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
附:![]()
独立性检验临界值表:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等式:sin25°+cos235°+sin 5°cos 35°=![]() ,
,
sin215°+cos245°+sin 15°cos 45°=![]() ,sin230°+cos260°+sin 30°·cos 60°=
,sin230°+cos260°+sin 30°·cos 60°=![]() ,…,由此归纳出对任意角度θ都成立的一个等式,并予以证明.
,…,由此归纳出对任意角度θ都成立的一个等式,并予以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4![]() 4:坐标系与参数方程
4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,其倾斜角为
,其倾斜角为![]() ,在以原点
,在以原点![]() 为极点,
为极点, ![]() 轴非负半轴为极轴的极坐标系中(取相同的长度单位),曲线C的极坐标方程为
轴非负半轴为极轴的极坐标系中(取相同的长度单位),曲线C的极坐标方程为![]() .
.
(Ⅰ)若直线![]() 与曲线C有公共点,求
与曲线C有公共点,求![]() 的取值范围;
的取值范围;
(Ⅱ)设![]() 为曲线C上任意一点,求
为曲线C上任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1}.
(1)若BA,求实数m的取值范围;
(2)当x∈R时,不存在元素x使x∈A与x∈B同时成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,焦点到短轴端点的距离为2,离心率为
轴上,焦点到短轴端点的距离为2,离心率为![]() .
.
(Ⅰ)求该椭圆的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点且
两点且![]() ,是否存在以原点
,是否存在以原点![]() 为圆心的定圆与直线
为圆心的定圆与直线![]() 相切?若存在求出定圆的方程;若不存在,请说明理由
相切?若存在求出定圆的方程;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com