若一三角形的重心与外接圆圆心重合,则此三角形为何种三角形?
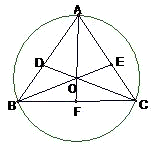
证明:设△ABC的重心与外接圆的圆心均为O(如图)
∵OA=OC,E为AC的中点,∴BE⊥AC;
同理,CD⊥AB,AF⊥BC
在Rt△ABE与Rt△ACD中,
∠A为公共角,BE=CD=R+

R=

R(R为外接圆半径),
所以△ABE≌△ACD,AB=AC,
同理可得AB=BC
由此可知△ABC为等边三角形.
分析:利用等腰三角形的中线与高重合,得到AF、BE、CD为三角形的高;利用全等三角形的判定定理得到两边相等,判断出三角形的形状.
点评:本题考查三角形的外心的性质、重心的性质、三角形全等的判定定理、据三角形的边角的关系判断出三角形的形状.
