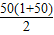练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    科技周活动中，数学老师展示出一个数字迷宫：将自然数1，2，3，4，…排成数阵，在2处转第1个弯，在3处转第2个弯，在5处转第3个弯，…，则第100个弯处的数是    ．
    【答案】分析：由图表观察可得：由1起每一个转弯时增加的数字可发现为“1，1，2，2，3，3，4，4，…”，由此结合等差数列的求和公式能求出在第100个转弯处的数．
    解答：解：观察由1起每一个转弯时增加的数字，
    可发现为“1，1，2，2，3，3，4，4，…”，
    即第一、二个转弯时增加的数字都是1，
    第三、四个转弯时增加的数字都是2，
    第五、六个转弯时增加的数字都是3，
    第七、八个转弯时增加的数字都是4，
    …
    故在第100个转弯处的数为：
    1+2（1+2+3+…+50）
    =1+2=2551．
    故答案为：2551．
    点评：本题考查等差数列的求和公式，对图表转弯处数字特征规律的发现是解决问题的关键，属基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    科技周活动中，数学老师展示出一个数字迷宫：将自然数1，2，3，4，…排成数阵，在2处转第1个弯，在3处转第2个弯，在5处转第3个弯，…，则第100个弯处的数是
    2551
    2551
    ．

    查看答案和解析>>

    科目：高中数学 来源：2013届河北省高二下学期第四次月考理科数学试卷（解析版） 题型：解答题

    （本小题满分12分）在我校值周活动中，甲、乙等五名值周生被随机地分到A，B，C，D四个不同的岗位服务，每个岗位至少有一名值周生．

    (1)求甲、乙两人同时参加A岗位服务的概率；

    (2)求甲、乙两人不在同一个岗位服务的概率；

    (3)设随机变量X为这五名值周生中参加A岗位服务的人数，求X的分布列及期望．

     

    查看答案和解析>>

    科目：高中数学 来源：2013届江苏南京学大教育专修学校高二五月理科数学试卷（解析版） 题型：解答题

    某次春游活动中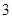，名老师和6名同学站成前后两排合影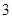，名老师站在前排，6名同学站在后排．

    （１）若甲，乙两名同学要站在后排的两端，共有多少种不同的排法？

    （２）若甲，乙两名同学不能相邻，共有多少种不同的排法？

    （３）若甲乙两名同学之间恰有两名同学，共有多少种不同的排法？

    （4）在所有老师和学生都排好后，拍照的师傅觉得队形不合适，遂决定从后排6人中抽2人调整到前排．若其他人的相对顺序不变，共有多少种不同的调整方法？

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

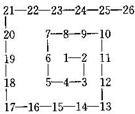    科技周活动中，数学老师展示出一个数字迷宫：将自然数1，2，3，4，…排成数阵，在2处转第1个弯，在3处转第2个弯，在5处转第3个弯，…，则第100个弯处的数是________．

    查看答案和解析>>

    同步练习册答案