
已知点(x,y)在直线x+2y=3上移动,则2x+4y的最小值是( )
A.8 B.6 C.3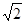 D.4
D.4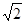
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 如图,在平面直坐标系xOy中,已知椭圆C:
如图,在平面直坐标系xOy中,已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 一青蛙从点A0(x0,y0)开始依次水平向右和竖直向上跳动,其落点坐标依次是Ai(xi,yi)(i∈N*),(如图所示,A0(x0,y0)坐标以已知条件为准),Sn表示青蛙从点A0到点An所经过的路程.
一青蛙从点A0(x0,y0)开始依次水平向右和竖直向上跳动,其落点坐标依次是Ai(xi,yi)(i∈N*),(如图所示,A0(x0,y0)坐标以已知条件为准),Sn表示青蛙从点A0到点An所经过的路程.| 1 |
| 2 |
| 1 |
| 2 |
| lim |
| n→+∞ |
| 1+8x |
| 1+8x |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建福州市毕业班质量检查文科数学试卷(解析版) 题型:解答题
已知椭圆C: 的离心率为
的离心率为 ,
,
直线 :y=x+2与原点为圆心,以椭圆C的短轴长为直
:y=x+2与原点为圆心,以椭圆C的短轴长为直
径的圆相切.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点 的直线
的直线 与椭圆
与椭圆 交于
交于 ,
, 两点.设直线
两点.设直线 的斜率
的斜率 ,在
,在 轴上是否存在点
轴上是否存在点 ,使得
,使得 是以GH为底边的等腰三角形. 如果存在,求出实数
是以GH为底边的等腰三角形. 如果存在,求出实数 的取值范围,如果不存在,请说明理由.
的取值范围,如果不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源:2011年上海市闵行区七宝中学高考数学模拟试卷(理科)(解析版) 题型:解答题
 ,试写出
,试写出 (不需证明);
(不需证明); 所表示的曲线上,要么落在
所表示的曲线上,要么落在 所表示的曲线上,并且A(0,4),求Sn的表达式.
所表示的曲线上,并且A(0,4),求Sn的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com