
设数列{an}:1,-2,-2,3,3,3,-4,-4,-4,-4,…,(-1)k-1k,…,(-1)k-1k,…,即当 <n≤
<n≤ (k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*).对于l∈N*,定义集合Pl={n|Sn是an的整数倍,n∈N*,且1≤n≤l}.
(k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*).对于l∈N*,定义集合Pl={n|Sn是an的整数倍,n∈N*,且1≤n≤l}.
(1)求集合P11中元素的个数;
(2)求集合P2 000中元素的个数.
(1)5 (2) 1 008
【解析】
解 (1)由数列{an}的定义得a1=1,a2=-2,a3=-2,a4=3,a5=3,a6=3,a7=-4,a8=-4,a9=-4,a10=-4,a11=5,所以S1=1,S2=-1,S3=-3,S4=0,S5=3,S6=6,S7=2,S8=-2,S9=-6,S10=-10,S11=-5,从而S1=a1,S4=0×a4,S5=a5,S6=2a6,S11=-a11,所以集合P11中元素的个数为5.
(2)先证:Si(2i+1)=-i(2i+1)(i∈N*).
事实上,①当i=1时,Si(2i+1)=S3=-3,-i(2i+1)=-3,故原等式成立;
②假设i=m时成立,即Sm(2m+1)=-m(2m+1),则i=m+1时 ,S(m+1)(2m+3)=Sm(2m+1)+(2m+1)2-(2m+2)2=-m(2m+1)-4m-3=-(2m2+5m+3)=-(m+1)(2m+3).
综合①②可得Si(2i+1)=-i(2i+1).于是
S(i+1)(2i+1)=Si(2i+1)+(2i+1)2=-i(2i+1)+(2i+1)2=(2i+1)(i+1).
由上可知Si(2i+1)是2i+1的倍数,而ai(2i+1)+j=2i+1(j=1,2,…,2i+1),所以Si(2i+1)+j=Si(2i+1)+j(2i+1)是ai(2i+1)+j(j=1,2,…,2i+1)的倍数.又S(i+1)(2i+1)=(i+1)·(2i+1)不是2i+2的倍数,而a(i+1)(2i+1)+j=-(2i+2)(j=1,2,…,2i+2),所以S(i+1)(2i+1)+j=S(i+1)(2i+1)-j(2i+2)=(2i+1)(i+1)-j(2i+2)不是a(i+1)(2i+1)+j(j=1,2,…,2i+2)的倍数,故当l=i(2i+1)时,集合Pl中元素的个数为1+3+…+(2i-1)=i2,于是,当l=i(2i+1)+j(1≤j≤2i+1)时,集合Pl中元素的个数为i2+j.
又2 000=31×(2×31+1)+47,故集合P2 000中元素的个数为312+47=1 008.


科目:高中数学 来源:2014年高考数学(理)二轮专题复习真题感悟1-7练习卷(解析版) 题型:填空题
将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习真题感悟1-3练习卷(解析版) 题型:填空题
设当x=θ时,函数f(x)=sin x-2cos x取得最大值,则cos θ=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习真题感悟1-1练习卷(解析版) 题型:填空题
若非零向量a,b满足|a|=3|b|=|a+2b|,则a与b夹角的余弦值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习真题感悟江苏专用常考问题4练习卷(解析版) 题型:填空题
抽样统计甲、乙两位射击运动员的5次训练成绩(单位:环),结果如下:
运动员 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
甲 | 87 | 91 | 90 | 89 | 93 |
乙 | 89 | 90 | 91 | 88 | 92 |
则成绩较为稳定(方差较小)的那位运动员成绩的方差为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习真题感悟江苏专用常考问题3练习卷(解析版) 题型:填空题
在平面直角坐标系xOy中,若双曲线 -
- =1的离心率为
=1的离心率为 ,则m的值为________.
,则m的值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习真题感悟江苏专用常考问题2练习卷(解析版) 题型:填空题
设当x=θ时,函数f(x)=sin x-2cos x取得最大值,则cos θ=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测4练习卷(解析版) 题型:解答题
设椭圆M: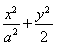 =1(a>
=1(a>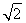 )的右焦点为F1,直线l:x=
)的右焦点为F1,直线l:x=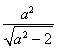 与x轴交于点A,若
与x轴交于点A,若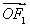 =2
=2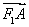 (其中O为坐标原点).
(其中O为坐标原点).
(1)求椭圆M的方程;
(2)设P是椭圆M上的任意一点,EF为圆N:x2+(y-2)2=1的任意一条直径(E,F为直径的两个端点),求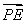 ·
·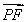 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com